Juggling notation facts for kids
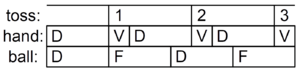
Juggling notation is a special way to write down juggling tricks and patterns. It helps jugglers share ideas with each other. Sometimes, it's hard to explain a juggling trick just by talking. Notation makes it much easier to understand and even discover new tricks!
The first idea for juggling notation came from Dave Storer in 1978. It was inspired by how music is written down. Later, in 1982, Jeff Walker created one of the first printed diagrams for juggling.
Contents
Types of Juggling Notation
Juggling notation usually comes in two main types: diagrams and numbers. Diagrams are visual, like pictures. Numeric systems use only numbers and letters.
Diagram-based Notation
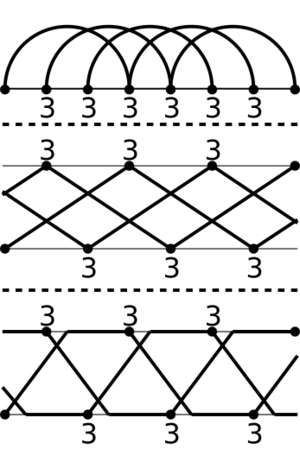
Diagrams are great because they show you what a juggling pattern looks like. They are easy to understand visually. However, they can be tricky to create and share using just text.
- Ladder diagrams - Think of these like a ladder. Each step or "rung" shows a moment in time. The lines on the ladder represent the juggling objects. They show how the objects move between a juggler's hands over time.
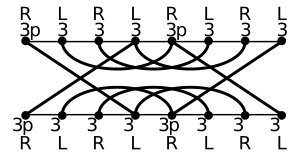
- Causal diagrams - These are a bit like ladder diagrams. But they don't show the props (like balls or clubs) being held. Instead, they show when a juggler needs to catch a prop. They also show what the juggler should do to make space in their hands. These are often used for club passing between jugglers.
- Mills Mess State Transition Diagrams - Mills Mess is a popular juggling pattern. In this trick, the juggler's arms cross over and uncross. These diagrams help track these arm movements.
Numeric Notation
Numeric systems use only numbers and common characters. This makes them easy to share through text messages or emails. Many numeric systems can also be used with computer programs. These programs can even animate the juggling patterns for you!
Siteswap
Siteswap is the most popular juggling notation system. It was created in 1985 by jugglers Bengt Magnusson and Bruce Boppo Tiemann.
A juggling pattern is shown as a series of numbers. For example, "333", "97531", or "744". Each number tells you how many "throws" happen before that same juggling prop is caught again.
Let's look at "333":
- This shows a common three-ball cascade.
- Each '3' means a prop is thrown.
- That same prop will be caught and thrown again after three throws have happened.
In a pattern like "531531":
- The '5' throw means the prop stays in the air for five throws.
- The '3' throw means the prop stays in the air for three throws.
- The '1' throw means the prop is passed directly to the other hand. It's thrown again on the very next throw.
The number also tells you how high you throw the prop. Or how long it stays in the air compared to other throws.
- Even numbers (like 2, 4, 6) usually mean the prop comes back to the same hand.
- Odd numbers (like 1, 3, 5) usually mean the prop crosses over to the other hand.
You can also figure out how many props are in a pattern. Just find the average of the numbers in one repeating group.
- "633633633" describes a four-prop pattern (average of 6, 3, 3 is 4).
- "414414414" describes a three-prop pattern (average of 4, 1, 4 is 3).
Types of Siteswap
"Vanilla" siteswap is the basic form. It uses simple numbers for patterns where you throw one prop at a time. You also alternate hands (left, then right, then left, etc.).
For more complex patterns, there are special siteswap extensions:
- Synchronous Siteswap (or "Synch" Siteswap) - This is for patterns where both hands throw at the exact same time. The numbers for both throws are put in parentheses. They are separated by a comma. For example, "(4,4)(4,4)(4,4)".
- Multiplex Siteswap - "Multiplex" means you throw more than one prop from the same hand at the same time. This siteswap lets you write down these patterns. You can even mix it with synchronous siteswap. A multiplex throw is shown with numbers in square brackets. For example, "23[43]23[43]" is a common four-ball multiplex pattern.
Vanilla, synch, and multiplex siteswap are the "standard" forms. Many jugglers understand them. Also, many computer programs can animate these patterns.
Other siteswap extensions exist for special uses. They are less common. Fewer jugglers know them, and they need special software.
- Passing siteswap - Used for simple passing patterns between jugglers.
- Multi-Hand Notation (MHN) - This system can describe patterns with any number of hands. It also works for different rhythms.
- Generalised Siteswap (GS) - This system uses a matrix (like a grid). It can describe many details about throws and catches. This includes timing, number of spins for clubs, or hand positions.