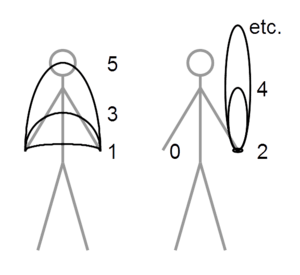Siteswap facts for kids
Siteswap is a special number code used to describe how people juggle. It's also called quantum juggling or the Cambridge notation. This code helps jugglers understand and create new juggling patterns. Each number in Siteswap tells you how many "beats" (or counts) in the future a juggling object will be thrown again. It mainly tracks when balls are thrown and caught.
Siteswap is super helpful for figuring out which groups of throws will make a real juggling pattern. It has even led to discovering new patterns, like "441". However, Siteswap doesn't describe body moves, like throwing a ball behind your back. It assumes that all throws happen at regular, even times.
For example, a common three-ball juggling pattern called a "cascade" is written as "3". A "shower" pattern, where balls go high in an arc, is written as "51".
Contents
How Siteswap Started
This clever way of writing juggling patterns was first thought up by Paul Klimek in Santa Cruz, California, in 1981. Later, students Bruce "Boppo" Tiemann and Bengt Magnusson at the California Institute of Technology helped develop it in 1985. Around the same time, Mike Day, Colin Wright, and Adam Chalcraft worked on it in Cambridge, England. That's why it's sometimes called the "Cambridge notation."
The name Siteswap comes from how you can create new patterns. You can "swap" when two throws are supposed to land. For example, if you swap the landing times of "5" and "1" in the pattern "51", you can create the pattern "24".
Basic Siteswap (Vanilla)
The simplest kind of Siteswap is called vanilla siteswap. It describes patterns where you throw balls from one hand to the other, switching hands each time. Also, you only throw one ball from each hand at a time.
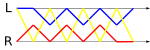
Imagine you are juggling while walking forward. The diagram on the right shows what it might look like from above. This is sometimes called a space-time diagram or ladder diagram. In this picture, three balls are being juggled. Time moves from the top to the bottom.
To describe a pattern, you count how many throws later each ball is caught. For example, the first throw in the diagram is a purple ball. It's thrown by the right hand. The purple ball is caught and thrown again by the left hand on the fifth throw. So, this first throw gets a count of 5. This creates a series of numbers that show how high each throw should be.
Since you switch hands, throws with odd numbers (like 3, 5, 7) send the ball to your other hand. Throws with even numbers (like 4, 6, 8) send the ball back to the same hand.
- A 3 means a throw to the opposite hand, like in a basic three-ball cascade.
- A 4 means a throw to the same hand, like in a four-ball fountain.
| Throw Name | Beats object is in Air | Switches hands | Description |
|---|---|---|---|
| 0 | - | - | Empty hand (you don't throw anything) |
| 1 | 1 | Yes | A quick pass from one hand to the other |
| 2 | 0 | No | Holding an object for a moment |
| 3 | 3 | Yes | A throw like in a 3-ball cascade |
| 4 | 4 | No | A throw like in a 4-ball fountain |
| 5 | 5 | Yes | A throw like in a 5-ball cascade |
| 6 | 6 | No | A throw like in a 6-ball fountain |
| 7 | 7 | Yes | A throw like in a 7-ball cascade |
| 8 | 8 | No | A throw like in an 8-ball fountain |
| 9 | 9 | Yes | A throw like in a 9-ball cascade |
| a | 10 | No | A throw like in a 10-ball fountain |
| b | 11 | Yes | A throw like in an 11-ball cascade |
| ... | ... | ... | ... |
There are three special throws:
- A 0 means you pause with an empty hand.
- A 1 is a quick pass straight to your other hand.
- A 2 means you hold an object for a moment.
Throws longer than 9 beats use letters like a, b, and so on. The number of beats a ball is in the air usually shows how high it was thrown. But it's more about the time in the air, not just the height. For example, bouncing a ball might take longer than throwing it to the same height.
Every Siteswap pattern repeats after a certain number of throws. This is called the period of the pattern. The period is the shortest number of digits that describe the repeating pattern. For example, the pattern shown in the diagram (53145305520) has 11 digits, so its period is 11.
If the period is an odd number, like 11, then each time the pattern repeats, you start with the other hand. This makes the pattern symmetrical, meaning both hands do the same things, just at different times. If the period is an even number, each hand does the same thing it did last time, and the pattern is asymmetrical.
The number of juggling objects (like balls) needed for a pattern is the average of the throw numbers in the pattern. For example, "441" is a three-object pattern because (4 + 4 + 1) / 3 equals 3. The pattern "86" is a seven-object pattern. All valid Siteswap patterns must have numbers that average out to a whole number. However, not all sequences that average to a whole number are valid. For instance, "543" averages to 4, but all three throws would land at the same time, causing them to crash!
Some jugglers like to write Siteswap patterns with the highest numbers first. But this isn't always the best way. For example, "51414" is a 3-ball pattern. You can't easily fit it into the middle of other 3-ball throws. But if you rotate it to "45141", you can.
Synchronous Siteswap
Siteswap can also describe patterns where you throw with both hands at the same time. This is called synchronous siteswap. The numbers for the two throws are put inside parentheses and separated by a comma. Since you throw with both hands at the same time, only even numbers are allowed. If a throw goes to the other hand, you add an x after the number.
For example, a synchronous three-object shower is written as (4x,2x). This means one hand throws a low ball (a 'zip') to the other hand, while the other hand throws a higher ball to the first hand. When you write a series of these pairs, you don't need extra marks between them. Patterns that repeat like a mirror image can be shortened with a *. For example, (4,2x)(2x,4) (which is a 3-ball box pattern) can be written as (4,2x)*.
Multiplexing
Siteswap can also show patterns where you throw more than one object from one or both hands at the same time. This is called a multiplex pattern. The numbers for multiple throws from one hand are put inside square brackets. For example, [33]33 is a normal 3-ball cascade, but two balls are always thrown together from one hand.
Passing
When two or more jugglers throw objects to each other, it's called passing. The <xxx|yyy> notation means one juggler does 'xxx' while another does 'yyy'. The letter 'p' is used for a throw that is passed to another juggler. For example, <3p 3|3p 3> is a 6-object passing pattern where all left-hand throws are passes, and all right-hand throws are kept by the same juggler. This can also be used with synchronous patterns. A two-person 'shower' could be <(4xp,2x)|(4xp,2x)>.
If the pattern has fractions, like <4.5 3 3 | 3 4 3.5>, it means the second juggler starts half a count later. All throws with fractions are passes. If both jugglers do the same pattern (just at different times), it's called a social siteswap. Then you only need to write half of the pattern. For example, <4p 3| 3 4p> becomes 4p 3.
Multi-handed Juggling
Ed Carstens created multi-hand notation in 1992 for his juggling program. Basic Siteswap (Vanilla) assumes you only throw one ball at a time. But Siteswap can also work for juggling with more than two hands, as long as the hands throw one after another.
- 1-handed (diabolo) Siteswap: This is when a single hand, or a diabolo player, throws diabolos to different heights.
- 4-handed Siteswap: This can be done by one juggler with four hands (if that were possible!) or by two jugglers working together with their four hands. The hands throw one after the other. Often, the jugglers take turns throwing. For example, the sequence might be: Right hand of Juggler A, Right hand of Juggler B, Left hand of Juggler A, Left hand of Juggler B.
State Diagrams
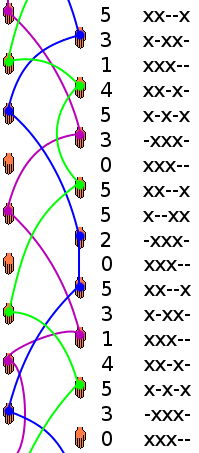
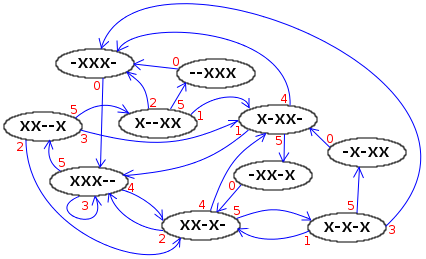
After you throw a juggling object, all the objects are in the air. Their landing times are already set. We can mark when a ball is going to land with an x and when there's no ball landing with a -. This shows the current state of the juggling pattern. It also tells you what kind of throw you can make next.
For example, look at the diagram. Just after the first throw, the state is xx--x. This means balls are landing soon, then there's a gap, then another ball lands. To figure out the next throw, we "catch" the ball that's landing first (the 'x' on the left). Then we shift everything else to the left and add a '-' on the right. So, xx--x becomes x--x-.
Since we just caught a ball, we can't throw a '0' (which means an empty hand). We also can't throw a '1' or a '4' because other balls are already scheduled to land at those times. If the highest you can throw is a '5', then you can only throw a '2', '3', or '5'. In the diagram, the juggler threw a '3'. So, an 'x' goes into the third spot, replacing the '-', and the new state becomes x-xx-.
The diagram shows all the possible states for juggling three objects with a maximum throw height of '5'. From each state, you can follow the arrows and numbers. These numbers create the Siteswap pattern. Any path that forms a loop (a cycle) in the diagram creates a valid Siteswap. All valid Siteswaps can be made this way. The diagram gets much bigger if you add more balls or higher throws.
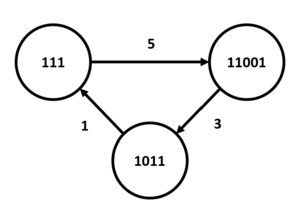
Another way to show Siteswap states is to use numbers. A ball landing is a '1' (instead of 'x'), and an empty spot is a '0' (instead of '-'). So, a state like xx--x could be 11001 in binary. This way, you can even show multiplex states, where a '2' means two balls land at that time.
|
Throw
State
|
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 111 | 111 | 1101 | 11001 | |||
| 0111 | 111 | |||||
| 1011 | 111 | 0111 | 01101 | |||
| 1101 | 111 | 1011 | 10101 | |||
| 00111 | 0111 | |||||
| 01011 | 1011 | |||||
| 01101 | 1101 | |||||
| 10011 | 1011 | 0111 | 00111 | |||
| 10101 | 1101 | 0111 | 01011 | |||
| 11001 | 1101 | 1011 | 10011 |
A Siteswap state diagram can also be shown as a state-transition table, like the one on the right. To create a Siteswap, you pick a starting state row. Then, you look at the column for the throw you want to make. The state shown where the row and column meet is your new state. You keep doing this. When you get back to your starting state, you've created a valid Siteswap pattern!
Mathematical Ideas in Siteswap
Is a Pattern Valid?
Not all Siteswap sequences are valid juggling patterns. A vanilla, synchronous, or multiplex Siteswap is valid if its state transitions create a loop (a cycle) in its state diagram. If it doesn't create a cycle, it's not valid. For example, the pattern "531" can be shown in a state diagram. Since its throws create a cycle, it's a valid pattern.
There are other ways to check if a pattern is valid, depending on the type of Siteswap.
For a vanilla Siteswap pattern like `a0 a1 a2 ... an-1` (where 'n' is how long the pattern is before it repeats), it's valid if all the balls land at different times. To check this, you can do a simple test:
- First, create a new list of numbers. Add 0 to the first number, 1 to the second, 2 to the third, and so on.
- Next, divide each number in this new list by the pattern's length ('n') and find the remainder.
- If all the remainders are different (no duplicates), then the pattern is valid!
Let's try "531". The pattern length ('n') is 3.
- First step: (5+0), (3+1), (1+2) which gives us 5, 4, 3.
- Second step (find remainders when divided by 3):
* 5 divided by 3 is 1 with a remainder of 2. * 4 divided by 3 is 1 with a remainder of 1. * 3 divided by 3 is 1 with a remainder of 0.
- The remainders are 2, 1, 0. Since all these numbers are unique, "531" is a valid pattern!
Now let's try "513". The pattern length ('n') is 3.
- First step: (5+0), (1+1), (3+2) which gives us 5, 2, 5.
- Second step (find remainders when divided by 3):
* 5 divided by 3 is 1 with a remainder of 2. * 2 divided by 3 is 0 with a remainder of 2. * 5 divided by 3 is 1 with a remainder of 2.
- The remainders are 2, 2, 2. Since the number 2 is duplicated, "513" is an invalid pattern. The balls would crash!
A synchronous Siteswap is valid if:
- It only uses even numbers for throws.
- It can be changed into a valid vanilla Siteswap using something called the "slide property" (explained next).
If it doesn't meet these rules, it's not valid.
Swap Property
You can create new valid vanilla Siteswap patterns by "swapping" two numbers next to each other in an existing valid pattern. When you swap them, you add 1 to the number that moves to the right and subtract 1 from the number that moves to the left.
For example, take the pattern "4413". If we swap the middle two throws (the '4' and the '1'):
- The '4' moves to the right, so it becomes 4-1 = 3.
- The '1' moves to the left, so it becomes 1+1 = 2.
This creates a new valid Siteswap pattern: "4233".
Slide Property
The "slide property" lets you change a valid synchronous Siteswap pattern into a valid asynchronous (vanilla) pattern, and vice versa. It's like sliding the throw times of one hand by one beat so that the throws don't happen at the same time anymore.
For example, the synchronous Siteswap "(8x,4x)(4,4)" can create two asynchronous (vanilla) Siteswaps using the slide property: "9344" and "5744".
Prime Patterns
Siteswap patterns can be either prime or composite. A Siteswap is prime if its path in the state diagram doesn't go through any state more than once. If it does, it's called composite.
A simpler way to think about it: a Siteswap is prime if you can't break it down into shorter, valid patterns that use the same number of juggling objects. For example, "44404413" is composite because you can split it into "4440", "441", and "3". But "441", which uses three objects, is prime. You can't break it into smaller valid 3-object patterns.
Sometimes this simple method doesn't work perfectly. For example, "153" (which is often written as "531") looks like it could be split into "15" and "3". But if you check its state diagram, you'll see it's actually a prime pattern.
It's been found that the longest prime Siteswaps often use mostly '0' (empty hand) and the highest possible throw number.
List of Symbols
- Number: Shows how high a throw is, like 1, 2, 3...
- Brackets []: Used for multiplex patterns, where multiple objects are thrown from one hand at once. Example: [333]33.
- Chevrons and vertical bar <|>: Used for patterns where jugglers throw at the same time or pass objects.
- P: Means a pass. Example: <333P|333P>
- Fraction: Means a pass that happens a fraction of a beat later. Example: <4.5 3 3 | 3 4 3.5>
- Parentheses (): Used for synchronous patterns, where both hands throw at the same time.
- *: Shortens a synchronous pattern that mirrors itself. Example: (4,2x)(2x,4) can be (4,2x)*
- x: Means a throw crosses to the other hand during a synchronous pattern.
Programs
Many free computer programs are available that can simulate juggling patterns using Siteswap. You can even find some games that use Siteswap!
|
See also
 In Spanish: Siteswap para niños
In Spanish: Siteswap para niños