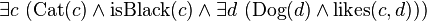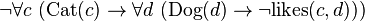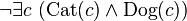Predicate logic facts for kids
In logic and philosophy, predicate logic is a special way of thinking about math and ideas. It helps us talk about things using "predicates." Think of a predicate as an incomplete sentence, like "is red" or "likes dogs." It needs a subject, like "The apple is red" or "My cat likes dogs," to become a complete idea.
Predicate logic is different from propositional logic because it uses something called "quantifiers." Quantifiers are words that tell us "how many" or "how much." They help us make statements about groups of things, not just single items.
The two most common quantifiers are:
- The existential quantifier, shown as ∃. This means "there exists at least one." For example, "∃ a cat" means "there is at least one cat." This statement is true if you can find even one cat.
- The universal quantifier, shown as ∀. This means "for all" or "every." For example, "∀ cats" means "for all cats" or "every cat." This statement is true only if *every single* cat fits the description.
In predicate logic, these quantifiers come before a variable (like x or y). This variable then stands for an object or person we are talking about. For example, the expression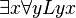 
can mean "There is a person x such that for all persons y, y likes x." In simpler words, "Someone is liked by everyone."
Contents
What are Predicates?
Predicates are like special functions that describe properties or relationships. They are usually written with a capital letter followed by variables in parentheses.
- `Cat(c)` means "c is a cat."
- `isBlack(c)` means "c is black."
- `likes(c,d)` means "c likes d."
These predicates become true or false depending on what you put in place of the variables.
Examples of Predicate Logic in Action
Let's look at some examples to see how predicate logic works.
Cats and Dogs
Imagine we want to say something about cats and dogs.
* This can be read as: "There is at least one cat (let's call it 'c') that is black, AND there is at least one dog (let's call it 'd') that the cat 'c' likes." * In simpler words: "There's a black cat that likes at least one dog."
* This one is a bit trickier! Let's break it down: * `Cat(c) \to \forall d\ (\text{Dog}(d) \to \neg\text{likes}(c,d))` means "IF 'c' is a cat, THEN for all dogs 'd', IF 'd' is a dog, THEN 'c' does NOT like 'd'." This means "Every cat doesn't like any dog." * The `\neg` at the beginning means "NOT." * So, the whole expression means: "It is NOT true that every cat doesn't like any dog." * In simpler words: "It's not true that no cat likes any dog." This means that at least one cat *does* like at least one dog!
* This means: "It is NOT true that there exists a 'c' such that 'c' is a cat AND 'c' is a dog." * In simpler words: "There is no animal that is both a cat and a dog." This makes sense!
Related pages
See also
In Spanish: Lógica de primer orden para niños
