Propositional logic facts for kids
Propositional logic is a way of thinking about statements and how they connect. It's like a special language used in mathematics and logic. You might also hear it called propositional calculus.
In propositional logic, we work with simple statements called propositions. A proposition is just a sentence that can be either completely true or completely false. For example, "The sky is blue" is a proposition because it's true. "Dogs can fly" is also a proposition, but it's false.
We often use capital letters like P, Q, or R to stand for these propositions. We can then link these simple statements together using special "joining words" called logical connectives. These connectives help us build more complex ideas.
Some common logical connectives are:
- AND (
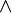 ): This means both statements must be true.
): This means both statements must be true. - OR (
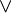 ): This means at least one of the statements must be true.
): This means at least one of the statements must be true. - IF...THEN (
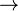 ): This shows a cause and effect.
): This shows a cause and effect. - IF AND ONLY IF (
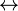 ): This means two statements are true or false together.
): This means two statements are true or false together. - NOT (
 ): This flips the truth of a statement (true becomes false, false becomes true).
): This flips the truth of a statement (true becomes false, false becomes true).
Propositional logic focuses on how these statements are connected, not on the details inside each statement. For example, if we say "All cats are dogs AND the Earth is a disc," propositional logic sees two separate statements joined by "AND." It doesn't care if "All cats are dogs" is silly!
Other types of logic build on propositional logic. For instance, predicate logic looks at parts of statements in more detail. Modal logic adds ideas like "it is possible that" or "it is necessary that."
Contents
Understanding "If-Then" Statements
A common type of statement in logic is an "if-then" statement, also known as an implication. It looks like "If P, then Q."
Let's use an example: "If it rains for an hour, then the ground will be wet."
- "P" is "it rains for an hour" (this is the first part, called the antecedent).
- "Q" is "the ground will be wet" (this is the second part, called the consequent).
For the whole "if-then" statement to be true, Q must happen if P is true. If P is true but Q doesn't happen, then the whole statement is false.
Here's a table showing when "If P, then Q" is true or false:
| P (First Statement) | Q (Second Statement) | Total Truth Value ("If P, then Q") |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | True |
| False | False | True |
You might notice something interesting in the table. If P is false, the "if-then" statement is always true, no matter what Q is. This is because the "if" condition wasn't met, so the statement isn't proven false.
Common Mistakes with "If-Then"
People often make two common mistakes when thinking about "if-then" statements:
- Mistake 1: "If Q, then P."
* Using our example: "If the ground is wet, then it has been raining for an hour." This isn't always true! The ground could be wet because someone spilled water, or snow melted.
- Mistake 2: "If not P, then not Q."
* Using our example: "If it has not been raining for an hour, then the ground is not wet." Again, this isn't always true. The ground could still be wet for other reasons, even if it didn't rain.
The only correct conclusion you can always make from "If P, then Q" is "If not Q, then not P."
- In our example: "If the ground is not wet, then it has not been raining for an hour." This must be true! If the ground isn't wet, then it couldn't have rained for an hour and made it wet.
Understanding "And" and "Or" Statements
Two other simple but important logical statements are those using "and" or "or."
- "P and Q"
* For this statement to be true, both P and Q must be true. If either P or Q (or both) are false, then "P and Q" is false. * Example: "The sun is shining AND it is daytime." This is only true if both parts are true.
- "P or Q"
* For this statement to be true, at least one of P or Q must be true. It's also true if both P and Q are true. The only time "P or Q" is false is if both P and Q are false. * Example: "Either I am in Hong Kong OR I am in London." This is true if you are in Hong Kong, or if you are in London, or if you somehow manage to be in both places at once (which isn't possible for a person, but logically, it would still make the "or" statement true!).
Related pages
See also
 In Spanish: Lógica proposicional para niños
In Spanish: Lógica proposicional para niños
 | Sharif Bey |
 | Hale Woodruff |
 | Richmond Barthé |
 | Purvis Young |

