Logical connective facts for kids
In logic, a logical connective is like a special "glue word" that connects different ideas or statements. You can also call them logical operators. They help us combine simple ideas into more complex ones. For example, in propositional logic, we can use the connective 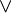 (which means "or") to join two simple statements, like "It is raining" (let's call it
(which means "or") to join two simple statements, like "It is raining" (let's call it 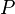 ) and "I am indoors" (let's call it
) and "I am indoors" (let's call it 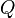 ). When we join them, we get
). When we join them, we get 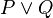 , which means "It is raining or I am indoors."
, which means "It is raining or I am indoors."
Some common logical connectives are "not," "or," "and," "if...then," and "if and only if." In standard classical logic, these connectives work like truth functions. This means their meaning depends only on whether the statements they connect are true or false. They are similar to words we use every day in English, but they are very precise in logic.
Contents
What are Logical Connectives?
In formal languages, which are like special languages used in math and computer science, logical connectives use clear symbols. This helps make sure that logical statements are always understood in the same way, without any confusion. These symbols are called logical connectives or logical operators.
Logical connectives can link different numbers of statements.
- Some connectives don't link any statements; they are just constants like "True" or "False." Think of them as always being true or always being false.
- Negation ("not") is a connective that works on one statement. For example, "not P" changes "P is true" to "P is false."
- Most connectives link two statements, like "and" or "or."
Here's a table showing some common connectives and how they work with "True" (1) and "False" (0):
Quick facts for kids Symbol, name |
Truth table |
Venn diagram |
||||||
|---|---|---|---|---|---|---|---|---|
| Zeroary connectives (constants) | ||||||||
| ⊤ | Truth (Always True) | 1 | ||||||
| ⊥ | Falsity (Always False) | 0 | ||||||
| Unary connectives | ||||||||
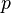 = = |
0 | 1 | ||||||
Statement  |
0 | 1 | ||||||
| ¬ | Negation (NOT) | 1 | 0 | |||||
| Binary connectives | ||||||||
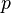 = = |
0 | 1 | ||||||
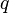 = = |
0 | 1 | 0 | 1 | ||||
Statement 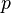 |
0 | 0 | 1 | 1 | ||||
Statement 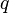 |
0 | 1 | 0 | 1 | ||||
| ∧ | Conjunction (AND) | 0 | 0 | 0 | 1 | |||
| ↑ | Alternative denial (NAND) | 1 | 1 | 1 | 0 | |||
| ∨ | Disjunction (OR) | 0 | 1 | 1 | 1 | |||
| ↓ | Joint denial (NOR) | 1 | 0 | 0 | 0 | |||
| → | Implication (IF...THEN) | 1 | 1 | 0 | 1 | |||
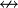 |
Exclusive or (XOR) | 0 | 1 | 1 | 0 | |||
| ↔ | Biconditional (IF AND ONLY IF) | 1 | 0 | 0 | 1 | |||
| ← | Converse implication (THEN...IF) | 1 | 0 | 1 | 1 | |||
| More information | ||||||||
Common Logical Connectives and Their Symbols
Here are the most common logical connectives you'll see:
- Negation (meaning "not"): The main symbol is
 . You might also see
. You might also see 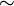 .
. - Conjunction (meaning "and"): The main symbol is
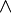 . You might also see
. You might also see 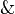 .
. - Disjunction (meaning "or"): The main symbol is
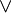 .
. - Implication (meaning "if...then"): The main symbol is
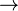 . You might also see
. You might also see  or
or  .
. - Equivalence (meaning "if and only if"): The main symbol is
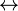 . You might also see
. You might also see  or
or 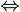 .
.
Let's use an example:
- Let
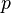 mean "It is raining."
mean "It is raining." - Let
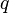 mean "I am indoors."
mean "I am indoors."
Here's how logical connectives change these statements:
- It is not raining (
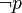 ).
). - It is raining and I am indoors (
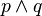 ).
). - It is raining or I am indoors (
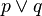 ).
). - If it is raining, then I am indoors (
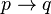 ).
). - I am indoors if and only if it is raining (
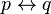 ).
).
We also have symbols for statements that are always true or always false:
- True formula:
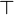 or
or 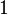 .
. - False formula:
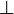 or
or 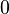 .
.
A Quick Look at History
The symbols we use for logical connectives have changed over time.
- The symbol for negation (
 ) appeared in 1930. The symbol
) appeared in 1930. The symbol 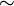 was used earlier, in 1908.
was used earlier, in 1908. - For conjunction (
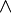 ), the symbol appeared in 1930. The
), the symbol appeared in 1930. The 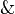 symbol was used even earlier, around 1924.
symbol was used even earlier, around 1924. - The symbol for disjunction (
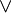 ) was used in 1908.
) was used in 1908. - For implication (
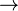 ), the symbol appeared in 1918.
), the symbol appeared in 1918. - The symbol for equivalence (
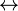 ) was used in 1933.
) was used in 1933.
Many of these symbols were developed by mathematicians and logicians like Arend Heyting, Bertrand Russell, David Hilbert, and Giuseppe Peano.
Why Some Connectives are "Redundant"
Sometimes, different logical statements can mean the same thing. For example, the statement "If P, then Q" (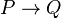 ) can actually be written using "not" and "or" as "Not P or Q" (
) can actually be written using "not" and "or" as "Not P or Q" (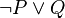 ).
).
This means that if you have "not" and "or" available, you don't strictly need "if...then." You can create the same meaning using a combination of other connectives. This idea is called "functional completeness." It means a small set of connectives can be used to build all other possible logical statements.
For example, you can create all logical statements using just the "NAND" ( ) connective, or just the "NOR" (
) connective, or just the "NOR" ( ) connective!
) connective!
Logical Connectives in Everyday Language
Logical connectives are similar to words we use in everyday language, like "and," "or," and "if...then." In English, these are often grammatical conjunctions. However, the meaning of these words in natural language isn't always exactly the same as their precise meaning in logic.
For example, when someone says "You can have cake or ice cream," they usually mean you can have one or the other, but not both (this is called an exclusive disjunction). In classical logic, "or" usually means you can have one, or the other, or both. These small differences are interesting to study in the field of formal semantics.
Here's a table showing how English words relate to logical connectives:
| English word | Connective | Symbol | Logic gate |
|---|---|---|---|
| not | negation |  |
NOT |
| and | conjunction | 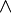 |
AND |
| or | disjunction | 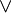 |
OR |
| if...then | material implication | 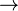 |
IMPLY |
| ...if | converse implication | 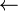 |
|
| if and only if | biconditional | 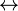 |
XNOR |
| not both | alternative denial | 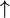 |
NAND |
| neither...nor | joint denial | 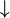 |
NOR |
| but not | material nonimplication |  |
NIMPLY |
Properties of Logical Connectives
Logical connectives have certain properties that help us understand how they work:
- Associativity: For some connectives, like "and" (
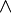 ) or "or" (
) or "or" (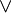 ), the order in which you group statements doesn't change the final meaning. For example, (A and B) and C means the same as A and (B and C).
), the order in which you group statements doesn't change the final meaning. For example, (A and B) and C means the same as A and (B and C). - Commutativity: For some connectives, you can swap the order of the statements without changing the meaning. For example, "A and B" means the same as "B and A."
- Distributivity: This is like how multiplication distributes over addition in math. For example, "A and (B or C)" is the same as "(A and B) or (A and C)."
- Idempotence: If you use the same statement twice with certain connectives, it's the same as just using it once. For example, "A and A" is the same as "A."
Order of Operations
Just like in math where you have an order of operations (like multiplication before addition), logical connectives also have an order of precedence. This helps us understand complex logical statements without needing too many parentheses.
Here's a common order, from highest precedence (done first) to lowest (done last):
| Operator | Precedence |
|---|---|
 (NOT) (NOT) |
1 (Highest) |
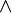 (AND) (AND) |
2 |
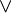 (OR) (OR) |
3 |
 (IF...THEN) (IF...THEN) |
4 |
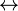 (IF AND ONLY IF) (IF AND ONLY IF) |
5 (Lowest) |
So, if you see 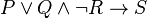 , it really means
, it really means 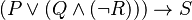 . The "NOT" happens first, then "AND," then "OR," and finally "IF...THEN."
. The "NOT" happens first, then "AND," then "OR," and finally "IF...THEN."
Logical Connectives in Computer Science
Logical connectives are super important in computer programming and how computers work!
- Logic Gates: In digital circuits, logical operators are built using logic gates. These are electronic circuits that perform logical operations like AND, OR, and NOT. Almost all digital circuits are made from these basic gates.
- Bitwise Operations: When computers work with numbers, they often use logical operators on bits (0s and 1s). These are called bitwise operations.
- Conditional Statements: In programming, "if...then" statements are like the logical implication. For example, `if (P) then Q;` means that if condition P is true, then action Q happens. If P is false, Q doesn't happen.
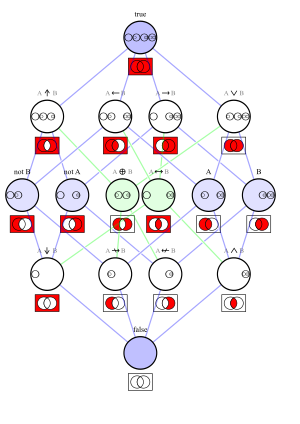
Table and Hasse Diagram
The 16 different logical connectives can be shown in a special diagram called a Hasse diagram. This diagram helps us see how they are related to each other based on when one statement implies another.
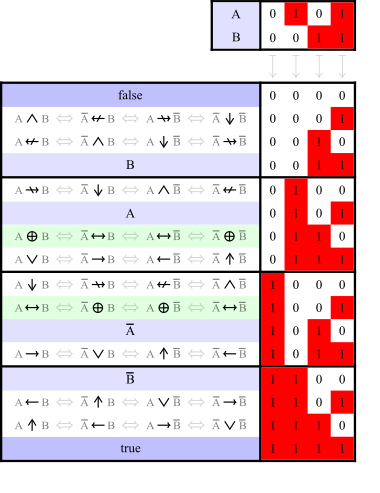 |
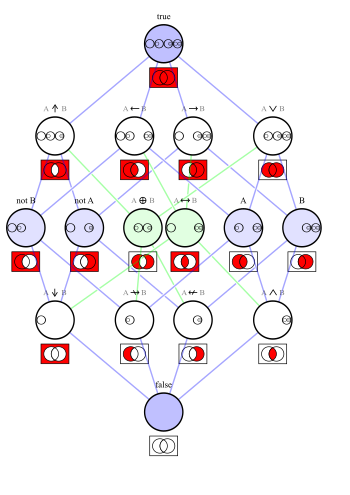 |
|
See also
 In Spanish: Conectiva lógica para niños
In Spanish: Conectiva lógica para niños
- Boolean logic
- Truth function
- Truth table
- Truth values
 | Jewel Prestage |
 | Ella Baker |
 | Fannie Lou Hamer |