Negation facts for kids
| NOT | |
|---|---|
 |
|
| Definition | 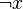 |
| Truth table | 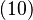 |
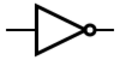
| Logic gate | |
| Normal forms | |
| Disjunctive | 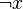 |
| Conjunctive | 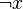 |
| Zhegalkin polynomial |  |
| Post's lattices | |
| 0-preserving | no |
| 1-preserving | no |
| Monotone | no |
| Affine | yes |
In logic, negation is a basic idea that means "the opposite of" or "not true". It's also called the logical not.
Imagine you have a statement, like "The sky is blue." Negation takes this statement and turns it into "The sky is not blue." If the first statement is true, its negation is false. If the first statement is false, its negation is true.
We often write negation using symbols like 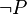 ,
, 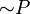 , or
, or 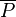 . The letter P here just stands for any statement. So,
. The letter P here just stands for any statement. So, 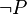 means "not P" or "P is not true."
means "not P" or "P is not true."
Contents
What is Negation?
Negation is a way to change the truth value of a statement. If a statement is true, its negation becomes false. If a statement is false, its negation becomes true.
For example:
- If the statement "It is raining" is true, then "It is not raining" is false.
- If the statement "The cat is flying" is false, then "The cat is not flying" is true.
This is how negation works in classical logic, which is the most common type of logic.
Truth Table for Negation
A truth table shows all possible outcomes for a logical operation. For negation, it's very simple:
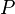 |
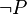 |
| True | False |
| False | True |
This table shows that if statement 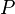 is true, then
is true, then 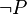 (not P) is false. If
(not P) is false. If  is false, then
is false, then 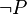 is true.
is true.
How to Write Negation
There are many ways to write or symbolize negation, depending on where you see it. Here are some common notations:
| Notation | Plain Text | How to say it |
|---|---|---|
 |
¬p , 7p | Not p |
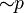 |
~p | Not p |
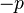 |
-p | Not p |
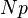 |
En p (This is from Polish notation) | |
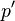 |
p' | p prime, or p complement |
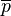 |
̅p | p bar, or Bar p |
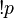 |
!p | Bang p, or Not p |
In Set theory, the symbol 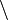 can mean "not in the set of." For example,
can mean "not in the set of." For example,  means "all members of set U that are not members of set A."
means "all members of set U that are not members of set A."
No matter how it's written, 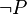 can always be read as "it is not the case that P," or simply "not P."
can always be read as "it is not the case that P," or simply "not P."
Key Properties of Negation
Double Negation
In classical logic, if you negate a statement twice, you get back to the original statement. This is called double negation. For example, "It is not true that it is not raining" means the same as "It is raining." In symbols, this is written as 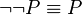 . The symbol
. The symbol  means "is logically the same as."
means "is logically the same as."
Distributing Negation (De Morgan's Laws)
De Morgan's laws show how negation works with "and" (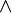 ) and "or" (
) and "or" (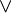 ) statements.
) statements.
- If you negate "P or Q," it's the same as "not P and not Q."
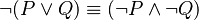
- If you negate "P and Q," it's the same as "not P or not Q."
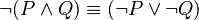
These laws are very useful in logic and computer science.
Negating Quantifiers
In first-order logic, we use quantifiers like "for all" (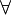 ) and "there exists" (
) and "there exists" (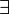 ). Negation changes these too:
). Negation changes these too:
- Negating "for all x, P is true" (
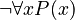 ) is the same as "there exists an x for which P is not true" (
) is the same as "there exists an x for which P is not true" (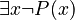 ).
).
* Example: "It is not true that all students are happy" means "Some student is not happy."
- Negating "there exists an x for which P is true" (
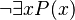 ) is the same as "for all x, P is not true" (
) is the same as "for all x, P is not true" (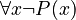 ).
).
* Example: "It is not true that some birds can't fly" means "All birds can fly."
Negation in Computer Programming
Negation is very important in computer science and programming languages. It helps computers make decisions.
For example, in many programming languages like C++, Java, and JavaScript, the exclamation mark "!" means logical NOT.
if (!(r == t)) // This means "if r is NOT equal to t"
{
// ... do something when r is not equal to t ...
}Many languages also have a shorter way to write "not equal to," like `!=`. So, `if (r != t)` means the same thing as `if (!(r == t))`.
Computers also use bitwise negation. This changes all the 1s to 0s and 0s to 1s in a binary number. This is used in low-level programming.
Here's another example of logical negation in programming:
unsigned int abs(int x)
{
if (!(x < 0)) // This means "if x is NOT less than 0" (so x is 0 or positive)
return x; // Return x as is
else
return -x; // If x IS less than 0 (negative), return its positive version
}This code finds the absolute value of a number. The `!(x < 0)` part is a logical negation. It means "it is not true that x is less than 0."
Sometimes, you might hear people use "!" in everyday talk, especially in computer-related slang. For example, "!voting" means "not voting," and "!clue" means "no clue" or "clueless."
Images for kids
- Affirmation and negation
- Bitwise NOT
- Contraposition
- Logical conjunction
- Logical disjunction
- NOT gate
- Truth function
- Truth table
See also
 In Spanish: Negación lógica para niños
In Spanish: Negación lógica para niños
 | Shirley Ann Jackson |
 | Garett Morgan |
 | J. Ernest Wilkins Jr. |
 | Elijah McCoy |