First-order logic facts for kids
First-order logic, also called predicate logic, is a way of thinking about and describing things using a special kind of language. It's like a powerful tool used in mathematics, philosophy, linguistics, and computer science.
Imagine you want to say "Socrates is a man." In simple logic, this is just one idea. But in first-order logic, you can say "there exists an 'x' such that 'x' is Socrates AND 'x' is a man." Here, "there exists" is a special word called a quantifier, and 'x' is a variable. This makes first-order logic much more detailed than propositional logic, which only deals with simple statements. Propositional logic is like the basic building block for first-order logic.
When we talk about a "theory" in first-order logic, it's like having a set of rules or ideas about a topic. For example, rules about set theory or number theory. These rules use first-order logic and apply to a specific group of things, called a domain of discourse. They also use special functions and properties, along with a set of starting rules called axioms.
The name "first-order" means we can talk about objects and their properties. But we can't talk about properties of properties. That's for "higher-order logic." In first-order logic, properties are often linked to sets of objects.
First-order logic is very important for setting up rules in mathematics. It's studied in the foundations of mathematics. Famous math systems like Peano arithmetic (for numbers) and Zermelo–Fraenkel set theory (for sets) are built using first-order logic. However, first-order logic can't perfectly describe infinite things like natural numbers or the real line. For that, you need stronger types of logic, like second-order logic.
The ideas behind first-order logic were developed by Gottlob Frege and Charles Sanders Peirce.
Contents
- What is First-Order Logic?
- How First-Order Logic is Built (Syntax)
- What First-Order Logic Means (Semantics)
- How to Prove Things (Deductive Systems)
- Equality and Its Rules
- Special Properties of First-Order Logic
- What First-Order Logic Can't Do (Limitations)
- Variations and Extensions
- Computers and Logic (Automated Theorem Proving)
- See also
What is First-Order Logic?
While propositional logic deals with simple statements that are either true or false, first-order logic goes further. It adds the idea of predicates (properties) and quantifiers (words like "all" or "some"). A predicate tells you if something is true or false for a specific object or objects.
Let's look at "Socrates is a philosopher" and "Plato is a philosopher." In simple propositional logic, these are just two separate statements. We might call them 'p' and 'q'. We don't think about them having a common part.
But in first-order logic, we see that both sentences say something about an individual. They both use the idea "is a philosopher." We can write this as "isPhil(x)," where 'x' stands for the person. For the first sentence, 'x' is "Socrates." For the second, 'x' is "Plato." Because first-order logic can talk about individual things, it includes all of propositional logic.
The truth of a statement like "x is a philosopher" depends on who 'x' is. It also depends on what "is a philosopher" means. So, "x is a philosopher" by itself isn't true or false. It's like a sentence fragment. We can connect these ideas using logical connectives. For example, "If x is a philosopher, then x is a scholar." This statement also needs 'x' to be defined to be true or false.
We can use quantifiers with variables. For instance, "For every x, if x is a philosopher, then x is a scholar." The universal quantifier "for every" means this idea is true for all possible choices of x.
The opposite of "For every x, if x is a philosopher, then x is a scholar" is "There exists x such that x is a philosopher and x is not a scholar." The existential quantifier "there exists" means this idea is true for at least one choice of x.
Predicates can also take more than one variable. For example, "Socrates is the teacher of Plato" uses the predicate "is the teacher of," which takes two variables.
An interpretation (or model) of a first-order statement tells us what each predicate means. It also defines the group of things that the variables can refer to. This group is called the domain of discourse or universe, and it must not be empty. For example, if our domain is all humans, and "is a philosopher" means "wrote the Republic", then "There exists x such that x is a philosopher" is true, because Plato wrote it.
First-order logic has two main parts:
- syntax: This tells us how to put symbols together correctly to form terms and statements.
- semantics: This gives meaning to those terms and statements.
How First-Order Logic is Built (Syntax)
The Alphabet of Logic
Just like English has an alphabet, first-order logic has its own set of symbols. These symbols are used to build terms and formulas. Terms are like names for objects, and formulas are like statements that can be true or false.
The symbols are divided into two groups:
- Logical symbols: These always mean the same thing. For example, the symbol for "and" always means "and."
- Non-logical symbols: Their meaning can change depending on what we are talking about. For example, a symbol like Phil(x) could mean "x is a philosopher" or "x is a person named Philip."
Logical Symbols
These symbols are always the same:
- Quantifiers:
* ∀ (means "for all" or "for every"). * ∃ (means "there exists" or "for some").
- Connectives: These join statements together.
* ∧ (for "and"). * ∨ (for "or"). * → (for "if...then..."). * ↔ (for "if and only if"). * ¬ (for "not").
- Punctuation: Like parentheses `()`.
- Variables: Letters like x, y, z, etc. We can add numbers to them, like x0, x1.
- Equality symbol: = (means "is equal to").
Not all these symbols are always needed. For example, you can express "for all" using "there exists" and "not."
Non-logical Symbols
These symbols represent specific things, properties, or actions. Their meaning changes with each topic.
- Predicate symbols: These describe properties or relationships. They are often uppercase letters like P, Q, R.
* P(x): Could mean "x is a man." * Q(x,y): Could mean "x is greater than y" or "x is the father of y." * A predicate with zero variables, like R, can stand for a simple statement, like "Socrates is a man."
- Function symbols: These represent actions or calculations. They are often lowercase letters like f, g, h.
* f(x): Could mean "the father of x" or "minus x" in math. * g(x,y): Could mean "x plus y" or "the union of x and y." * A function symbol with zero variables is called a constant symbol. These are like specific names or numbers, such as a, b, c. For example, 'a' could stand for Socrates, or 0 in arithmetic.
The specific set of non-logical symbols used for a topic is called a signature. For example, for groups in math, the signature might be `{1, ×}`.
How to Build Terms and Formulas
The rules for putting symbols together are very precise. This makes sure that every expression is well-formed and has only one meaning.
Terms
Terms are like nouns in a sentence; they refer to objects.
- Variables: Any variable symbol (like x) is a term.
- Functions: If f is a function symbol (like 'father of') and t1, ..., tn are terms, then f(t1,...,tn) is a term. Constant symbols (like 'Socrates') are also terms because they are functions with zero inputs.
Formulas
Formulas are like complete sentences; they express statements that can be true or false.
- Predicates: If P is a predicate symbol (like 'is a philosopher') and t1, ..., tn are terms, then P(t1,...,tn) is a formula.
- Equality: If t1 and t2 are terms, then t1 = t2 is a formula.
- Negation: If
 is a formula, then
is a formula, then 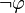 (not
(not  ) is a formula.
) is a formula. - Binary Connectives: If
 and
and 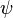 are formulas, then (
are formulas, then ( ) (if
) (if  then
then 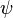 ) is a formula. The same applies to "and," "or," and "if and only if."
) is a formula. The same applies to "and," "or," and "if and only if." - Quantifiers: If
 is a formula and x is a variable, then
is a formula and x is a variable, then 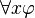 (for all x,
(for all x,  is true) and
is true) and 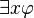 (there exists x such that
(there exists x such that  is true) are formulas.
is true) are formulas.
Formulas made only by the first two rules (predicates and equality) are called atomic formulas.
For example, 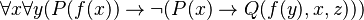 is a formula if 'f' is a one-input function, 'P' is a one-input predicate, and 'Q' is a three-input predicate. But
is a formula if 'f' is a one-input function, 'P' is a one-input predicate, and 'Q' is a three-input predicate. But 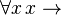 is not a formula because it doesn't follow the rules.
is not a formula because it doesn't follow the rules.
Parentheses are important to make sure each formula can only be understood in one way. This is called unique readability.
Reading Formulas Easily
To make formulas easier to read, we have rules for which operations happen first, like in math.
- "Not" (
 ) is done first.
) is done first. - "And" (
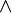 ) and "or" (
) and "or" (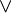 ) are next.
) are next. - Quantifiers (
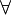 ,
, 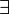 ) are next.
) are next. - "If...then..." (
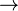 ) is last.
) is last.
Sometimes, we write things like "2 + 2 = 4" instead of "=(+(2,2),4)". This is called infix notation and is just a shortcut for the more formal way.
Free and Bound Variables
In a formula, a variable can be free or bound.
- A variable is bound if it's "controlled" by a quantifier. For example, in ∀y P(x, y), the variable y is bound by
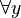 .
. - A variable is free if it's not bound by any quantifier. In ∀y P(x, y), the variable x is free.
Think of it like this: if you say "He is tall," "He" is a free variable; you don't know who "he" is. But if you say "Every boy is tall," "boy" is bound by "every," so you know it applies to all boys.
A formula with no free variables is called a first-order sentence. Sentences have a definite true or false value. For example, "Phil(x)" isn't true or false until you know who 'x' is. But the sentence ∃x Phil(x) ("There exists an 'x' such that 'x' is a philosopher") is either true or false in a given situation.
What First-Order Logic Means (Semantics)
Interpretation is about giving meaning to the symbols in first-order logic. It's like defining what each word in a language means. It also sets up a domain of discourse, which is the group of all the "objects" we are talking about.
First-Order Structures
The most common way to give meaning is to create a structure (also called a model). A structure has:
- A domain of discourse (D): This is a non-empty set of "objects." For example, it could be all integers.
- An interpretation function (I): This function gives meaning to the non-logical symbols.
* An n-input function symbol (like 'f') becomes a real function that takes n objects from D and gives back one object from D. For example, 'f' could mean "addition" if D is integers. * A constant symbol (like 'c') becomes a specific object in D. For example, 'c' could mean the number 10. * An n-input predicate symbol (like 'P') becomes a set of n-tuples of objects from D. If an n-tuple is in the set, the predicate is true for those objects. For example, 'P' could mean "is less than," and it would be true for pairs like (2, 5).
Finding Truth Values
A formula becomes true or false based on the interpretation and a variable assignment (μ). This assignment tells us which object in the domain each variable refers to. For example, if we have the formula 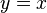 , its truth depends on what x and y stand for.
, its truth depends on what x and y stand for.
Here's how truth values are found:
- Terms: Each term (like a variable or a function applied to terms) gets assigned a specific object from the domain.
- Atomic Formulas:
* A formula like  is true if the objects that
is true if the objects that 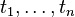 refer to are in the set that P means. * A formula like
refer to are in the set that P means. * A formula like  is true if
is true if 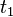 and
and 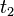 refer to the exact same object.
refer to the exact same object.
- Logical Connectives: Formulas with "not," "and," "or," etc., are evaluated using truth tables, just like in propositional logic.
- Existential Quantifiers:
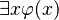 is true if there is at least one way to pick an object for x from the domain that makes
is true if there is at least one way to pick an object for x from the domain that makes 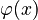 true.
true. - Universal Quantifiers:
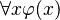 is true if
is true if 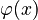 is true for every possible object you pick for x from the domain.
is true for every possible object you pick for x from the domain.
If a formula is a sentence (no free variables), its truth value doesn't depend on the variable assignment. It's either true or false for that interpretation.
Validity and Logical Consequence
- A sentence is satisfiable if there is at least one interpretation where it is true.
- A formula is logically valid if it is true in every possible interpretation. These are like the "always true" statements.
- A formula
 is a logical consequence of another formula
is a logical consequence of another formula 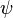 if whenever
if whenever 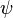 is true,
is true,  is also true.
is also true.
First-Order Theories and Models
A first-order theory is a set of starting rules (axioms) for a specific topic. For example, the rules for groups or ordered fields. A structure that makes all the rules in a theory true is called a model of that theory.
Many theories have an intended interpretation, which is the specific model we usually think of. For example, for Peano arithmetic, the intended interpretation is the usual natural numbers. But the Löwenheim–Skolem theorem shows that most first-order theories also have other, unexpected models.
A theory is consistent if you can't prove a contradiction (like "true and false") from its rules. A theory is complete if, for any statement, you can either prove it or prove its opposite. Gödel's incompleteness theorem shows that if a first-order theory is strong enough to describe natural numbers, it can't be both consistent and complete.
How to Prove Things (Deductive Systems)
A deductive system is a set of rules for showing that one formula logically follows from another, just by looking at their symbols. There are many types of these systems. They all share the idea that a proof is a finite, step-by-step process.
A deductive system is sound if everything you can prove in it is actually logically true. It is complete if you can prove every logically true statement in it. All the systems for first-order logic are both sound and complete. This means they work perfectly.
The cool thing about deductive systems is that they are purely about symbols. You don't need to understand what the symbols mean to check if a proof is correct. So, a correct argument works no matter if you're talking about math, economics, or anything else.
In general, figuring out if one first-order statement logically implies another is "semidecidable." This means if it *does* imply it, you'll eventually find a proof. But if it *doesn't*, you might never know for sure, because you could keep searching for a proof forever.
Rules of Inference
A rule of inference is a guideline that says: if you have a certain formula, you can write down another specific formula as a conclusion. The rule is good if it always keeps the truth.
For example, the rule of substitution says that if you have a formula  with a variable x, you can replace all free x's with a term t to get
with a variable x, you can replace all free x's with a term t to get ![\varphi[''t''/''x'']](/images/math/0/a/b/0abb003c0f63218a985f660887a679aa.png) . But you have to be careful that no new variables accidentally get "bound" by a quantifier during this process.
. But you have to be careful that no new variables accidentally get "bound" by a quantifier during this process.
Rules of inference are purely about symbols. You can check if they are applied correctly without knowing what the symbols mean.
Hilbert-Style Systems and Natural Deduction
- Hilbert-style systems: A proof is a list of formulas. Each formula is either a basic logical rule (axiom), something you assumed to be true, or it comes from previous formulas using a rule. These systems usually have a few rules but many basic axioms.
- Natural deduction systems: These are similar but have no basic axioms. Instead, they have more rules for how to handle the logical connections in formulas.
Resolution
The resolution rule is a single rule that, with another process called unification, is sound and complete for first-order logic. It's often used in automated theorem proving, where computers try to find proofs.
Resolution works by trying to show that the opposite of what you want to prove is impossible.
Common Identities
Many identities (equivalences) can be proven. These help rearrange formulas. For example:
- "Not for all x, P(x)" is the same as "There exists an x such that not P(x)":

- "Not there exists an x, P(x)" is the same as "For all x, not P(x)":

- "For all x, for all y, P(x,y)" is the same as "For all y, for all x, P(x,y)":

Equality and Its Rules
Equality (the `=` symbol) can be handled in a few ways. The most common way is first-order logic with equality. Here, `=` is a basic logical symbol that always means "is the exact same thing as." This approach also adds special rules (axioms) for equality:
- Reflexivity: Everything is equal to itself (x = x).
- Substitution for functions: If x = y, then if you use x or y in a function, the result will be the same.
- Substitution for formulas: If x = y, then any statement true about x is also true about y. This is also known as Leibniz's law.
Other properties of equality, like:
- Symmetry: If x = y, then y = x.
- Transitivity: If x = y and y = z, then x = z.
are consequences of these basic axioms.
First-Order Logic Without Equality
Another way is to treat equality as a non-logical symbol. This is called first-order logic without equality. If you want equality in your theory, you have to add its axioms yourself. The main difference is that in this case, two different objects could be "equal" according to your theory, even if they are not truly the same object.
Special Properties of First-Order Logic
First-order logic has many special properties that stronger logics don't have. These properties are about first-order logic itself, not about specific theories. They are very useful for building models (interpretations) of theories.
Completeness and Undecidability
- 'Gödel's completeness theorem (1929) says that there are perfect proof systems for first-order logic. This means if a statement logically follows from another, you can always find a proof for it.
- However, first-order logic is 'undecidable (though semidecidable). This means there's no computer program that can always tell you if any given formula is logically true or not. This was shown by Alonzo Church and Alan Turing in the 1930s.
The Löwenheim–Skolem Theorem
This theorem says that if a first-order theory has an infinite model (an interpretation with infinitely many objects), then it has models of every infinite size. This means you can't use first-order logic to describe something as being "countable" or "uncountable" in a unique way.
For example, there's no first-order theory that only has the real numbers as its model. Any theory that works for the real numbers will also work for other, stranger infinite models.
The Compactness Theorem
The compactness theorem states that if an infinite set of first-order sentences has a model, then every finite part of that set also has a model. This means if a formula is a logical consequence of an infinite set of rules, it's actually a consequence of just a few of those rules. This theorem is a key tool in model theory for building new models.
This theorem also limits what kinds of collections of structures can be described by first-order logic. For example, the set of all finite graphs cannot be described by a single first-order theory.
What First-Order Logic Can't Do (Limitations)
Even though first-order logic is powerful, it has some limits.
Expressiveness
The Löwenheim–Skolem theorem shows that first-order logic can't uniquely describe infinite things like the natural numbers or real numbers. Stronger logics, like infinitary logics or higher-order logics, can do this. But these stronger logics lose some of the nice properties that first-order logic has, like the compactness theorem.
Describing Natural Languages
First-order logic can describe many simple sentences from everyday language, like "Every person who lives in Perth lives in Australia." It's used in knowledge representation languages for computers.
However, some complex parts of natural language are hard or impossible to express in first-order logic. For example:
- Quantifying over properties: You can't easily say "John has at least one thing in common with Peter" if that "thing" is a property.
- Adverbs: "John is walking quickly" is hard to break down. "Quickly" isn't just another property of John.
- Relative adjectives: "Jumbo is a small elephant" is tricky. "Small" here depends on "elephant." Jumbo might be small for an elephant, but huge for a mouse.
Variations and Extensions
There are many different versions of first-order logic. Some just change the symbols, while others add new features that make the logic more powerful.
Simpler Languages
You can simplify first-order logic by using fewer symbols. For example:
- You only need one quantifier (either "for all" or "there exists") because you can define one using the other and "not."
- You only need "not" and "or" (or "not" and "and") as connectives, because you can define the others from these.
- You can even avoid function symbols and constant symbols by using predicates instead.
These simplifications make it easier to prove things about the logic itself, but they make it harder to write down everyday statements.
Many-Sorted Logic
Normal first-order logic has one big group of objects for all variables. Many-sorted first-order logic lets variables have different "sorts" or "types," each with its own group of objects. For example, you could have a sort for "numbers" and a sort for "people."
If there are only a few sorts, you can turn many-sorted logic into regular first-order logic. You just add a special predicate for each sort (e.g., 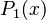 for "x is a number") and then use these predicates to limit your statements.
for "x is a number") and then use these predicates to limit your statements.
Additional Quantifiers
You can add new quantifiers:
- Uniqueness quantification:
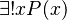 means "there is exactly one x such that P(x) is true."
means "there is exactly one x such that P(x) is true." - Extra quantifiers: Like "there are many x such that..."
- Bounded quantifiers: Used in set theory or arithmetic to talk about elements within a certain range.
Infinitary Logics
Infinitary logic allows formulas that are infinitely long. For example, you could have an "and" statement with infinitely many parts. These are used in advanced math areas like topology.
Non-Classical and Modal Logics
- Intuitionistic first-order logic: This uses a different kind of reasoning where, for example, "not not true" doesn't always mean "true."
- First-order modal logic: This adds ideas of "possibility" and "necessity." It lets you talk about different "possible worlds" where things might be true or false.
- First-order fuzzy logics: These deal with statements that are not just true or false, but can be true to a certain degree (like "mostly true").
Higher-Order Logics
The main feature of first-order logic is that you can only quantify over individual objects. You can say "there exists a person," but not "there exists a property." Second-order logic lets you quantify over properties (predicates) too. Other higher-order logics go even further, allowing quantification over relations between relations, and so on. The "first" in "first-order logic" tells you what kind of things you can count.
Higher-order logics are more powerful. For example, they can uniquely describe the natural numbers or real numbers. But this power comes at a cost: they don't have some of the nice properties of first-order logic, like the Löwenheim–Skolem theorem or the compactness theorem.
Computers and Logic (Automated Theorem Proving)
Automated theorem proving is about making computer programs that can find formal proofs for mathematical theorems. This is very hard because there are so many possible proofs to check. So, programmers create smart ways (heuristics) to help the computer search faster.
Another related area is automated proof verification. Here, computers check if proofs written by humans are correct. These systems are often smaller and simpler, so their own correctness can be checked.
Some proof checkers, like Metamath, need the whole proof step-by-step. Others, like Mizar and Isabelle, take a detailed outline and fill in the missing parts. Many of these systems are used by mathematicians to help them write very precise proofs.
Automated theorem provers are also used in formal verification in computer science. They help check if computer programs and hardware (like processors) work exactly as they are supposed to. This is very important for things where a mistake could be dangerous or very expensive.
See also
 In Spanish: Lógica de primer orden para niños
In Spanish: Lógica de primer orden para niños
- Aristotelian logic
- List of logic symbols
- Prolog
- Truth table
 | Leon Lynch |
 | Milton P. Webster |
 | Ferdinand Smith |

