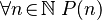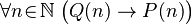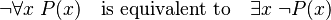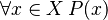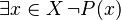Universal quantification facts for kids

In mathematical logic, a universal quantification is a way to say something is true for everything in a group. Think of it as saying "for all" or "for every". It means a certain statement is true for every single thing in a specific group you are talking about. It's like saying a certain feature or connection applies to everyone or everything in that group.

This idea is shown using the symbol 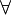, which looks like a turned "A". When you see "∀x", it means "for all x". This is called the universal quantifier. It's different from existential quantification (which means "there exists at least one"). Existential quantification only says the property is true for one or more things, not necessarily all.

You can find more about how these ideas work in the article on quantification (logic). The universal quantifier symbol 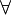is also known as Error using : Input "2200" is not a hexadecimal value. in Unicode. You can type it as \forall in programs like LaTeX.

What is Universal Quantification?

Imagine you have a list of math facts:

• 2 times 0 equals 0 plus 0
• 2 times 1 equals 1 plus 1
• 2 times 2 equals 2 plus 2

...and so on.

This list uses "and" many times. But how do you write "and so on" in a clear, formal way? In formal logic, we can't just say "etc." Instead, we use universal quantification. We would say: "For all natural numbers n, 2 times n equals n plus n."

This statement is much clearer. It tells us exactly what kind of numbers n can be (natural numbers). This example is true because if you pick any natural number for n, the statement "2·n = n + n" will always be true.

Now, let's look at a different example: "For all natural numbers n, 2 times n is greater than 2 plus n."

This statement is false. Why? Because if you pick n as 1, then "2·1 > 2 + 1" becomes "2 > 3", which is false. Even if the statement is true for most numbers, just one example where it's false (called a counterexample) makes the whole universal statement false.

The Importance of the Group You're Talking About

What if we change the group of numbers we're talking about? "For all composite numbers n, 2 times n is greater than 2 plus n."

This statement is actually true! A composite number is a number that can be divided evenly by numbers other than 1 and itself (like 4, 6, 8, 9...). The number 1 is not a composite number, so it's not a counterexample here. This shows how important it is to define the domain of discourse, which is the specific group of things n can be.

When the group is limited, we often use an "if...then" statement. For example, the statement above is the same as saying: "For all natural numbers n, if n is a composite number, then 2 times n is greater than 2 plus n." The "if ... then" part is called a logical conditional.

How to Write Universal Quantification

In symbolic logic, we use the symbol 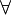for universal quantification. Gerhard Gentzen first used it in 1935.

For example, let's say P(n) means "2 times n is greater than 2 plus n". And let N be the set of natural numbers. Then, we write:

This means: "for all natural numbers n, P(n) is true." (Which we know is false).

Now, let Q(n) mean "n is a composite number". We can write:

This means: "for all natural numbers n, if n is a composite number, then 2 times n is greater than 2 plus n." (Which we know is true).

There are other ways to write these symbols, which you can find in the Quantifier article.

How Universal Quantification Works

Negating a Universal Statement

If you want to say that a universal statement is not true, you change the universal quantifier (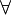) to an existential quantifier (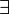) and then say the original statement is false. So, saying "it is not true that for all x, P(x) is true" is the same as saying "there exists an x for which P(x) is not true." We write this as:

Here, means "not".

Let's use an example. Imagine P(x) means "x is married". Let X be the set of all living people. The statement "Every living person x is married" is written as:

This statement is false. So, we want to say it's not true: "It is not true that every living person x is married." Or, in symbols:

.

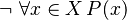Since it's not true that every person is married, it must mean there's at least one person who is not married. So, the opposite of "all are married" is "at least one is not married." This is written as:

It's important not to get confused!

• "All persons are not married" means "no one is married."
• "Not all persons are married" means "some people are not married."

These are very different!

Rules for Using Universal Quantifiers

In logic, there are rules for how you can use universal quantifiers in arguments. These are called rules of inference.

• Universal instantiation (or Universal Elimination): If you know something is true for everything in a group, then it must be true for any specific thing in that group.

For example, if you know "All birds have feathers," then you can say "My pet parrot has feathers." In symbols: 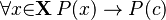 : This means: if P(x) is true for all x in group X, then P(c) is true for any specific c from group X.

• Universal generalization (or Universal Introduction): If you can show that a statement is true for any random thing you pick from a group, then you can say it's true for everything in that group.

For example, if you pick any triangle and show its angles add up to 180 degrees, then you can say "All triangles have angles that add up to 180 degrees." In symbols: 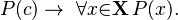 : This means: if P(c) is true for any random c, then P(x) is true for all x in group X. The c must be truly random; if you picked a specific example (like your pet parrot), you couldn't say it's true for all birds.

What About Empty Groups?

If the group you are talking about is empty (it has no members), then a universal statement about it is always considered true. This is called a vacuous truth. For example, "All unicorns in this room are purple" is true if there are no unicorns in the room.

Images for kids

• 

  A robot thinking about logic.

See Also

• Existential quantification
• First-order logic
• List of logic symbols—for the Unicode symbol ∀