Quantifier (logic) facts for kids

Kids Encyclopedia Facts

In logic, a quantifier is a special symbol or word that tells us "how many" things in a group fit a certain description. Think of it like saying "all" or "some."

For example, in first-order logic, the universal quantifier (symbol: 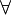$\forall$ ) means "for all" or "every." If you see 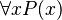Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \forall x P(x) , it means "every single thing (x) in our group has the property P."

On the other hand, the existential quantifier (symbol: 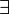$\exists$ ) means "there exists" or "at least one." So, 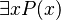$\exists x P(x)$ means "there is at least one thing (x) in our group that has the property P."

When a quantifier is the main part of a logical statement, it's called a quantified formula. These formulas always have a bound variable (a variable tied to the quantifier) and a smaller part that describes what that variable is doing.

Table of truth for Existential and Universal quantifiers.

The most common quantifiers are 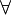$\forall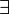$ (for all) and $\exists$ (there exists). In classical logic, you can even define one using the other with negation (like "not"). For instance, "nothing has property P" can be written as 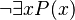Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \neg \exists x P(x) (it's not true that there exists an x with property P).

In first-order logic, if you have two "for all" quantifiers or two "there exists" quantifiers next to each other, you can swap their order without changing the meaning. But if you swap a "for all" with a "there exists," the meaning usually changes. For example, the definitions of uniform continuity and (ordinary) continuity in math are different just because of the order of quantifiers.

Quantifiers help us describe things in a precise way, similar to how we use words like "some" and "all" in everyday language.

Quantifiers and Logical Connections
Symbols and How We Write Them
Order of Quantifiers (Nesting)
Equivalent Ways to Write Quantifiers
Range of Quantification
Other Types of Quantifiers
History of Quantifiers
See also

Quantifiers and Logical Connections

Imagine you have a small group of items, like 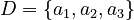Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): D = \{a_1, a_2, a_3\} .

Universal Quantifier (For All)

When we say "for all x in D, P(x) is true" (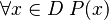 $\forall x \in D \; P(x)$ ), it's like saying:

P(a1) is true AND P(a2) is true AND P(a3) is true.

This is called a logical conjunction because everything must be true.

For example, if 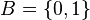Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): B = \{0, 1\} (the numbers 0 and 1), the statement 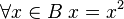$\forall x \in B \; x = x^2$ means:

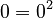Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 0 = 0^2 (which is true) AND 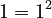Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 = 1^2 (which is true).

Since both parts are true, the whole statement is true.

Existential Quantifier (There Exists)

When we say "there exists an x in D such that P(x) is true" (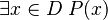 $\exists x \in D \; P(x)$ ), it's like saying:

P(a1) is true OR P(a2) is true OR P(a3) is true.

This is called a logical disjunction because at least one part needs to be true.

Infinite Groups

What if our group is infinite, like all natural numbers? We can't list them all. For example, instead of writing:

1 · 2 = 1 + 1, and 2 · 2 = 2 + 2, and 3 · 2 = 3 + 3, and so on...

We can use a universal quantifier:

For each natural number n, n · 2 = n + n.

Similarly, for "there exists": Instead of:

1 is equal to 5 + 5, or 2 is equal to 5 + 5, or 3 is equal to 5 + 5, and so on...

We can use an existential quantifier:

For some natural number n, n is equal to 5+5.

Symbols and How We Write Them

The main symbols for quantifiers are:

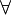$\forall$ (a rotated "A") for "for all" or "every."
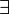$\exists$ (a rotated "E") for "there exists" or "at least one."

Let's try translating a sentence into logic: "Each of Peter's friends either likes to dance or likes to go to the beach (or both)."

We can break this down:

Let X be the group of all Peter's friends.
Let P(x) mean "x likes to dance."
Let Q(x) mean "x likes to go to the beach."

Then the sentence becomes: 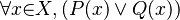Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \forall{x}{\in}X, (P(x) \lor Q(x)) . This reads: "For every x that is a member of X, P applies to x or Q applies to x."

Here are some other ways you might see quantifiers written:

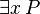Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \exists{x}\, P (There exists an x such that P is true)
$\forall{x}\, P$ (For all x, P is true)

You might also see variations like:

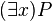
$(\exists{x}) P$
$\exists x \ \cdot \ P$
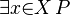$\exists{x}{\in}X \, P$ (meaning "there exists an x in the set X")

It's important to always know what group of things the variable (like 'x') is referring to. This is called the range of quantification or domain of discourse. Sometimes it's clear from the problem, or it's stated directly. For example, "For every natural number x..."

Order of Quantifiers (Nesting)

The order of quantifiers really matters! Swapping them can completely change the meaning of a statement.

Let's look at an example: 1. For every natural number n, there exists a natural number s such that s = n². * This means that for any number n you pick (like 1, 2, 3...), you can always find its square (1, 4, 9...). This statement is true.

2. There exists a natural number s such that for every natural number n, s = n². * This means there's one special number s that is the square of *every* natural number. This is impossible! No single number can be the square of 1, 2, 3, and so on, all at once. This statement is false.

See how just changing the order of "for every" and "there exists" makes a huge difference?

Another example comes from mathematical analysis with continuous and uniformly continuous functions. Their definitions look very similar, but the order of quantifiers is swapped, which changes their meaning.

A function f is pointwise continuous if:

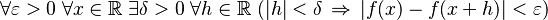$\forall \varepsilon > 0 \; \forall x \in \R \; \exists \delta > 0 \; \forall h \in \R \; (|h| < \delta \, \Rightarrow \, |f(x) - f(x + h)| < \varepsilon )$ Here, the value of 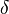$\delta$ can depend on both $\varepsilon$ and $x$ .

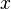A function f is uniformly continuous if:

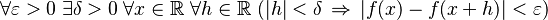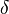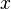$\forall \varepsilon > 0 \; \exists \delta > 0 \; \forall x \in \R \; \forall h \in \R \; (|h| < \delta \, \Rightarrow \, |f(x) - f(x + h)| < \varepsilon )$ Here, the value of $\delta$ can only depend on $\varepsilon$ , not on $x$ . This is a stronger condition.

Generally, if you swap two "for all" quantifiers next to each other, or two "there exists" quantifiers next to each other, the meaning stays the same. But swapping a "for all" and a "there exists" can change the meaning.

The "depth" of nested quantifiers (how many are inside each other) is called its "quantifier rank".

Equivalent Ways to Write Quantifiers

Sometimes, you can write the same idea in different ways using quantifiers and other logical symbols.

If D is the group of things for x, and P(x) is a statement about x, then:

"For all x in D, P(x) is true" can be written as:

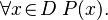$\forall x\!\in\!D\; P(x).$ Or, it can be written as: 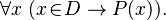$\forall x\;(x\!\in\!D \to P(x)).$ (This means "for all x, if x is in D, then P(x) is true.")

"There exists an x in D such that P(x) is true" can be written as:

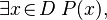$\exists x\!\in\!D\; P(x),$ Or, it can be written as: 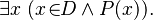$\exists x\;(x\!\in\!\!D \land P(x)).$ (This means "there exists an x such that x is in D AND P(x) is true.")

Quantifiers are also linked to negation (the "not" operator):

To show that "not all x in D have property P" is true, you just need to find one x in D that does NOT have property P.

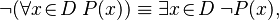
$\neg (\forall x\!\in\!D\; P(x)) \equiv \exists x\!\in\!D\; \neg P(x),$

To show that "there does not exist an x in D with property P" is true, you need to show that for all x in D, they do NOT have property P.

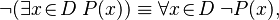
$\neg (\exists x\!\in\!D\; P(x)) \equiv \forall x\!\in\!D\; \neg P(x),$

Range of Quantification

Every time you use a quantifier, you need to know what group of things the variable is talking about. This group is called the domain of discourse or range of quantification.

For example, saying "some number is even" means different things if you're talking about natural numbers (1, 2, 3...) versus real numbers (numbers with decimals).

Sometimes, the domain is fixed for a whole mathematical theory. For instance, in Zermelo–Fraenkel set theory, variables always refer to "sets." If you want to talk about natural numbers, you'd say: "For every n, if n belongs to the set of natural numbers (N), then n·2 = n + n."

If the range of quantification is empty (meaning there are no items in the group), then:

A "for all" statement is always true (because there are no items to make it false).
A "there exists" statement is always false (because nothing exists in an empty group).

Other Types of Quantifiers

While "for all" and "there exists" are the most common, other types of quantifiers exist.

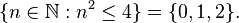For example, the "solution quantifier" (symbol: §) is used to describe a set of solutions. $\left[ \S n \in \mathbb{N} \quad n^2 \leq 4 \right] = \{0, 1, 2\}$ This reads: "Those n in the set of natural numbers (N) such that n² is less than or equal to 4 are the numbers {0, 1, 2}." This is similar to set-builder notation: $\{n \in \mathbb N: n^2 \le 4\} = \{0, 1, 2\}.$ Unlike other quantifiers, this one gives you a set as an answer, not just a true/false statement.

Other ideas that act like quantifiers include:

"There are infinitely many elements such that..."
"For all but finitely many elements..." (meaning almost all elements)

History of Quantifiers

Term logic, developed by Aristotle around the 4th century BC, was an early form of logic that dealt with ideas like "All," "Some," and "No." It was closer to how we speak naturally.

The modern idea of a "quantifier" was first used by Augustus De Morgan in 1862. He talked about "all" and "some-not-all" as quantifiers.

Augustus De Morgan (1806-1871) was the first to use "quantifier" in the modern sense.

However, it was Gottlob Frege in his 1879 book Begriffsschrift who first used a quantifier symbol to "bind" a variable. He used a special symbol for "for all." He didn't have a symbol for "there exists" but used a trick with negation to mean the same thing. Frege's ideas weren't widely known until Bertrand Russell wrote about them in 1903.

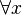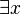Later, Charles Sanders Peirce and his student Oscar Howard Mitchell independently came up with their own symbols for universal and existential quantifiers. Peirce used Π_x and Σ_x, which are similar to our modern $\forall x$ and $\exists x$ . Peirce's notation was used by famous logicians like Kurt Gödel.

Giuseppe Peano also created his own notation, using (x) for "for all x" and ∃x for "there exists x." Peano's notation became very popular in Europe and was used in the famous Principia Mathematica by Whitehead and Russell.

The symbol 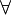$\forall$ that we use today was introduced by Gentzen in 1935, similar to Peano's 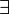$\exists$ symbol. It didn't become the standard until the 1960s.