Modal logic facts for kids
Modal logic is a special kind of logic that helps us talk about things that are necessary or possible. It's like adding special words to our sentences to say if something must be true, or if it could be true.
This type of logic is very important in philosophy and other areas. It helps us understand ideas like knowledge, what we should do (obligations), and how things cause other things to happen.
For example, in a type of modal logic about knowledge, a special symbol (like a box,  ) can mean "it is known that". So,
) can mean "it is known that". So, 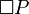 would mean "it is known that P is true". In another type of modal logic about duties, the same box symbol could mean "it is a moral duty that P is true".
would mean "it is known that P is true". In another type of modal logic about duties, the same box symbol could mean "it is a moral duty that P is true".
Modal logic looks at how these "modal" statements connect. For instance, many logics about knowledge say that if something is known ( ), then it must be true (
), then it must be true (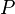 ). You can't know something that isn't true!
). You can't know something that isn't true!
Modal logics use special symbols like  (diamond) for "possibly" and
(diamond) for "possibly" and  (box) for "necessarily". So,
(box) for "necessarily". So, 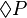 means "possibly P", and
means "possibly P", and 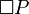 means "necessarily P".
means "necessarily P".
A common way to understand modal logic is through "possible worlds". Imagine different versions of reality. A statement like 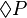 (possibly P) is true if P is true in at least one of these possible worlds that we can "reach" from our current world. A statement like
(possibly P) is true if P is true in at least one of these possible worlds that we can "reach" from our current world. A statement like 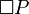 (necessarily P) is true if P is true in every possible world we can reach.
(necessarily P) is true if P is true in every possible world we can reach.
The idea of modal logic has been around for a long time. But the first formal systems were created by C. I. Lewis in 1912. The idea of "possible worlds" for understanding these logics came later, in the mid-1900s, from people like Arthur Prior and Saul Kripke. Today, modal logic is used in many fields, including game theory, moral and legal theory, and even web design.
What are Modal Operators?
Modal logic is different because it uses special symbols called modal operators. The main ones are  (box) and
(box) and  (diamond).
(diamond).
The box symbol  usually means "necessarily". It can stand for ideas like:
usually means "necessarily". It can stand for ideas like:
- Something that must happen (like a moral rule).
- Something that is known to be true.
- Something that is certain to happen.
The diamond symbol  usually means "possibly". It can stand for ideas like:
usually means "possibly". It can stand for ideas like:
- Something that is allowed (like permission).
- Something that you can do (ability).
- Something that fits with the evidence you have.
In modal logic, you can have simple statements like 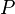 (which means "P is true"). But you can also have modal statements like
(which means "P is true"). But you can also have modal statements like 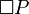 (P is necessary) or
(P is necessary) or 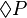 (P is possible). You can even combine them, like
(P is possible). You can even combine them, like 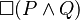 (it's necessary that P and Q are true).
(it's necessary that P and Q are true).
The basic rules for building statements in modal logic are:
- If
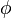 is a simple statement, then
is a simple statement, then 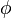 is a valid statement.
is a valid statement. - If
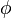 is a valid statement, then
is a valid statement, then 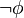 (not
(not 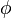 ) is also valid.
) is also valid. - If
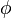 and
and 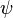 are valid statements, then
are valid statements, then 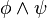 (
(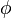 and
and 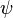 ) is also valid.
) is also valid. - If
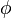 is a valid statement, then
is a valid statement, then 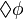 (possibly
(possibly 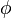 ) is also valid.
) is also valid. - If
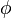 is a valid statement, then
is a valid statement, then  (necessarily
(necessarily 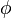 ) is also valid.
) is also valid.
Sometimes,  can be defined using
can be defined using  as "not possibly not
as "not possibly not 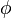 " (
" ( ). This means if something is necessary, it's not possible for it to be false.
). This means if something is necessary, it's not possible for it to be false.
Other symbols are used too. For example, ![[K]](/images/math/5/f/f/5ff406fb8f2c6bd8eee29c3988cf1967.png) might mean "it is known that" and
might mean "it is known that" and 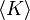 might mean "it is consistent with what is known that". You can even have many operators, like
might mean "it is consistent with what is known that". You can even have many operators, like  ,
,  , for different types of necessity.
, for different types of necessity.
How Modal Logic Works (Semantics)
Relational Semantics: Possible Worlds
The most common way to understand modal logic is called relational semantics. It uses the idea of "possible worlds".
Basic Ideas
In this approach, whether a statement is true depends on which "possible world" we are talking about. If a statement has a modal operator (like  or
or  ), its truth can also depend on what is true in other possible worlds that are "accessible" from the current one.
), its truth can also depend on what is true in other possible worlds that are "accessible" from the current one.
To do this, we use a "model" that has three parts:
- A set of possible worlds (let's call them W). Think of these as different ways things could be.
- An accessibility relation (R). This is a rule that tells us which worlds are "reachable" from other worlds. For example, if world 'u' is accessible from world 'w', it means 'u' is a possible situation given what's true in 'w'.
- A valuation function (V). This function tells us which simple statements are true in which worlds.
So, how do we decide if a statement is true in a world 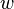 in our model?
in our model?
- A simple statement
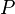 is true in world
is true in world 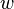 if our function
if our function 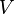 says it's true there.
says it's true there. 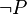 (not P) is true in world
(not P) is true in world 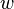 if
if 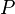 is not true in
is not true in 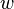 .
.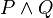 (P and Q) is true in world
(P and Q) is true in world 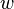 if both
if both 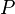 and
and 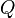 are true in
are true in 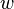 .
.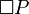 (necessarily P) is true in world
(necessarily P) is true in world 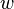 if
if 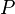 is true in every world
is true in every world 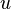 that is accessible from
that is accessible from 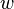 .
.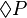 (possibly P) is true in world
(possibly P) is true in world 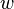 if
if 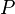 is true in at least one world
is true in at least one world 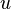 that is accessible from
that is accessible from 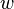 .
.
This means "necessary" depends on what's true in all reachable worlds. "Possible" depends on what's true in some reachable world. This helps us show that possibility isn't always the same. For example, it's not physically possible to travel faster than light, given our laws of physics. But it might be logically possible in a different kind of world.
Frames and Different Logics
The rules for the accessibility relation 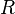 can change what statements are true. For example, if every world can "see" itself (meaning
can change what statements are true. For example, if every world can "see" itself (meaning 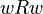 is always true), then if something is necessary, it must be true in that world.
is always true), then if something is necessary, it must be true in that world.
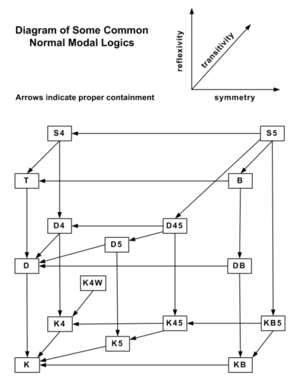
Different types of modal logic are built by setting different rules for the accessibility relation. These rules are called "frame conditions":
- Reflexive: Every world can see itself (w R w).
- Symmetric: If world w can see world u, then u can also see w (w R u means u R w).
- Transitive: If w can see u, and u can see q, then w can also see q (w R u and u R q means w R q).
- Serial: From every world w, there is at least one world u that w can see (w R u).
These conditions lead to different systems of modal logic:
- K: No special conditions.
- D: The relation is serial.
- T: The relation is reflexive.
- S4: The relation is reflexive and transitive.
- S5: The relation is reflexive and symmetric and transitive (this means all worlds can see each other, or are grouped into fully connected parts).
Axiomatic Systems: Building Modal Logics with Rules
The first ways to define modal logic were through axiomatic systems. This means starting with a few basic truths (axioms) and rules, and then proving other truths from them.
Modern modal logic usually starts with propositional calculus (basic logic about "and", "or", "not"). Then, it adds the box ( ) and diamond (
) and diamond ( ) operators.
) operators.
In classical modal logic, these two operators are linked:
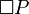 ("necessarily P") is the same as
("necessarily P") is the same as 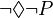 ("not possibly not P").
("not possibly not P").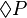 ("possibly P") is the same as
("possibly P") is the same as 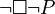 ("not necessarily not P").
("not necessarily not P").
This means they are a "dual pair" – you can define one using the other.
Many modal logics, called normal modal logics, include these two important rules:
- Necessitation Rule (N): If a statement p is a proven truth, then
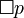 (it is necessary that p) is also a proven truth.
(it is necessary that p) is also a proven truth. - Distribution Axiom (K):
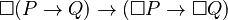 . This means if it's necessary that (P leads to Q), then if P is necessary, Q must also be necessary.
. This means if it's necessary that (P leads to Q), then if P is necessary, Q must also be necessary.
The simplest normal modal logic is called "K" (named after Saul Kripke). It only has the basic logic, plus the N rule and the K axiom.
You can create other well-known modal systems by adding more axioms to K:
- T (Reflexivity Axiom):
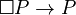 (If P is necessary, then P is true). This axiom is true in most modal logics.
(If P is necessary, then P is true). This axiom is true in most modal logics. - 4:
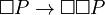 (If P is necessary, then it's necessary that P is necessary).
(If P is necessary, then it's necessary that P is necessary). - 5:
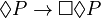 (If P is possible, then it's necessary that P is possible).
(If P is possible, then it's necessary that P is possible). - D:
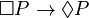 (If P is necessary, then P is possible).
(If P is necessary, then P is possible).
These axioms lead to systems like:
- T: K + T
- S4: T + 4
- S5: T + 5
- D: K + D
These systems (K through S5) form a hierarchy, meaning each one is stronger than the last. S5 is a very strong system where all modal truths are considered necessary.
Modal Logics in Philosophy
Modal logic is used to understand different kinds of "modality" or ways of being.
Alethic Logic: Necessity and Possibility
This is the original type of modal logic. It deals with what is necessary and possible in a very general sense.
- Something is possible if it's not necessarily false. It could be true, even if it's not true right now.
- Something is necessary if it's not possibly false. It must be true.
- Something is contingent if it's possible but not necessary. It could be true, but it could also be false.
- Something is impossible if it's not possibly true. It cannot be true.
Think of "possible worlds" again. Something "necessary" is true in all possible worlds. Something "possible" is true in at least one possible world.
Physical Possibility
Something is physically possible if the laws of physics allow it. For example, it's physically possible for a new element to exist, even if we haven't found it yet. But according to modern science, it's not physically possible to travel faster than the speed of light.
Metaphysical Possibility
This type of possibility is about what could be true about the basic nature of things, even beyond physical laws. For example, some philosophers think it's metaphysically necessary that all thinking beings have bodies. Saul Kripke argued that you necessarily have the parents you do; if you had different parents, you wouldn't be the same person.
Metaphysical possibility is often seen as more strict than just logical possibility. Philosophers debate if these truths are just "by definition" or if they show deep facts about the world.
Epistemic Logic: Logic of Knowledge
Epistemic modalities deal with how certain we are about statements. The  operator here means "x is certain that..." or "x knows that...". The
operator here means "x is certain that..." or "x knows that...". The  operator means "For all x knows, it may be true that...".
operator means "For all x knows, it may be true that...".
It's important to tell the difference between epistemic (what we know) and metaphysical (what could be true in reality) possibility.
- If you say, "It's not possible that Bigfoot exists; I'm certain of that," you're making an epistemic claim. You mean, based on what you know, it's not true.
- If you say, "Sure, it's possible that Bigfoots could exist," you're making a metaphysical claim. You mean there's no physical reason they couldn't exist, even if they don't.
Epistemic possibilities affect our actions. If someone tells you, "It's possible that it's raining outside" (epistemic), you might take an umbrella. But if they say, "It's possible for it to rain outside" (metaphysical), that doesn't help you decide about the umbrella.
Temporal Logic: Logic of Time
Temporal logic deals with statements about when things happen. Some things are always true (like 2+2=4). Other things are only true sometimes (like "John is happy").
In temporal logic, we use operators for the past and future:
- FP: It will sometimes be the case that P.
- GP: It will always be the case that P.
- PP: It was sometime the case that P.
- HP: It has always been the case that P.
We can say that "possibly it will rain tomorrow" and "possibly it won't". But if it rained yesterday, it's not possible that it didn't rain yesterday. The past seems "fixed" or necessary, in a way the future is not.
Temporal logic is also used in computer science to model how computer programs work. For example, 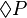 might mean "at some future point in the program, P will be true".
might mean "at some future point in the program, P will be true".
Deontic Logic: Logic of Duty and Rules
Deontic logic deals with what we ought to do, or what is permitted. The difference between "You must do this" and "You may do this" is like the difference between "This is necessary" and "This is possible".
In deontic logic,  means "it is obligatory that" and
means "it is obligatory that" and  means "it is permitted that". A common idea in deontic logic is that "ought implies can". This means if you ought to do something, then you can do it. This is often represented by the axiom D:
means "it is permitted that". A common idea in deontic logic is that "ought implies can". This means if you ought to do something, then you can do it. This is often represented by the axiom D: 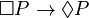 (If P is obligatory, then P is permitted).
(If P is obligatory, then P is permitted).
Doxastic Logic: Logic of Belief
Doxastic logic is about the logic of belief. The  operator (often written as 'B') means "It is believed that". So,
operator (often written as 'B') means "It is believed that". So, 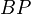 means "It is believed that P is true".
means "It is believed that P is true".
Metaphysical Questions: What are Possible Worlds?
When we talk about "logically possible worlds" in modal logic, what do we really mean? If a statement is true in all possible worlds, it's a necessary truth. If it's true in our world but not all possible worlds, it's a contingent truth.
For example, if we say "Bigfoot's existence is possible but not actual," we mean "There is some possible world where Bigfoot exists, but in our actual world, Bigfoot does not exist."
But are these "possible worlds" real places, just like our own? Saul Kripke thought "possible world" was just a helpful way to imagine possibility, not that these worlds actually exist. David Lewis, however, believed that all possible worlds are just as real as our own. This idea is called "modal realism". Other philosophers try to explain modal logic without saying that possible worlds are real.
In computer science, "all worlds" might mean "all possible next steps of the computer" or "all possible future states of the computer."
Other Uses
Modal logics are also being used in other areas like literature, poetry, art, and history to understand different ways of thinking and storytelling.
History of Modal Logic
The basic ideas of modal logic go way back to ancient times. Aristotle talked about necessity and possibility in his writings. Later, in the Middle Ages, thinkers like William of Ockham and John Duns Scotus used modal ideas to discuss important philosophical concepts.
Modern modal logic really started with C. I. Lewis in 1912. He created the first formal systems, including the well-known S1 through S5 systems.
For a while, modal logic didn't get much attention. But in 1959, Saul Kripke, who was only 18 at the time, introduced the "possible worlds" semantics (now called Kripke semantics). This made modal logic much easier to understand and work with.
Later, Arthur Norman Prior created modern temporal logic in 1957, which is closely related to modal logic. It added operators for "eventually" and "previously". Temporal logic is now very important in computer science for analyzing how programs behave.
The mathematical side of modal logic also grew, showing its connections to Boolean algebra and topology.
See also
 In Spanish: Lógica modal para niños
In Spanish: Lógica modal para niños
- Accessibility relation
- Conceptual necessity
- Counterpart theory
- David Kellogg Lewis
- De dicto and de re
- Description logic
- Doxastic logic
- Dynamic logic
- Enthymeme
- Free choice inference
- Hybrid logic
- Interior algebra
- Interpretability logic
- Kripke semantics
- Metaphysical necessity
- Modal verb
- Multimodal logic
- Multi-valued logic
- Neighborhood semantics
- Provability logic
- Regular modal logic
- Relevance logic
- Strict conditional
- Two-dimensionalism
 | Emma Amos |
 | Edward Mitchell Bannister |
 | Larry D. Alexander |
 | Ernie Barnes |