Prime gap facts for kids

Prime gap frequency distribution for primes up to 1.6 billion. Peaks occur at multiples of 6.

A prime gap is the space or difference between two prime numbers that come right after each other. Think of it like skipping numbers on a number line. If you have a prime number, the next prime number might be very close, or it might be quite far away. The n-th prime gap, often called g_n, is simply the result of subtracting the n-th prime number from the next one (the (n + 1)-st prime).

For example:

The first prime number is 2. The next is 3. The gap is 3 - 2 = 1. So, g₁ = 1.
The next prime after 3 is 5. The gap is 5 - 3 = 2. So, g₂ = 2.
The next prime after 5 is 7. The gap is 7 - 5 = 2. So, g₃ = 2.
The next prime after 7 is 11. The gap is 11 - 7 = 4. So, g₄ = 4.

Mathematicians have studied these prime gaps a lot. However, there are still many puzzles and ideas (called conjectures) about them that haven't been solved yet.

Here are the first few prime gaps: 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ...

Cool Facts About Prime Gaps
Measuring Prime Gaps
- Record-Breaking Gaps
- Maximal Gaps
Big Ideas and Unsolved Puzzles
- How Big Can Gaps Be?
- How Small Can Gaps Be?
Conjectures: What Mathematicians Believe (But Can't Prove Yet)
See also

Cool Facts About Prime Gaps

The very first prime gap is 1, which is between the primes 2 and 3. This is the only gap that is an odd number. All other prime gaps are even numbers. This is because, except for 2, all prime numbers are odd. If you subtract an odd number from another odd number, you always get an even number.

There's only one time when two gaps in a row are both 2. This happens with the primes 3, 5, and 7. The gap between 3 and 5 is 2, and the gap between 5 and 7 is also 2.

Finding Really Big Gaps

Did you know that you can find prime gaps that are as big as you want? It's true! For any number you pick, there's a prime gap that's even bigger than that number.

Here's a simple idea to show this: Imagine you pick a number, say 5. The factorial of 5 (written as 5!) means 5 × 4 × 3 × 2 × 1 = 120. Now look at the numbers right after 120:

120 + 2 = 122 (divisible by 2)
120 + 3 = 123 (divisible by 3)
120 + 4 = 124 (divisible by 4)
120 + 5 = 125 (divisible by 5)

All these numbers (122, 123, 124, 125) are composite numbers (not prime). This means there's a gap of at least 4 numbers that are not prime. This sequence of non-prime numbers must be part of a prime gap. This idea works for any number, so you can always find a gap as large as you want.

However, these really big gaps don't always appear where you might expect them. For example, the first prime gap larger than 14 is between 523 and 541. That's a gap of 18. But 15! is a huge number (1,307,674,368,000)!

Average Gap Size

As prime numbers get larger, the average space between them also tends to get larger. It grows roughly with the natural logarithm of the prime number. This means that even though the gaps get bigger, they get smaller in proportion to the size of the primes themselves.

Twin Primes

A special idea called the twin prime conjecture suggests that there are infinitely many prime gaps of size 2. These are called twin primes, like (3, 5), (5, 7), (11, 13), and so on. It's one of the biggest unsolved mysteries in math!

Measuring Prime Gaps

Mathematicians use something called "merit" to compare how big a prime gap is compared to the average gap size around that prime. A higher merit means the gap is unusually large for primes of that size.

The largest known prime gap found so far (as of March 2024) has a length of 16,045,848! It's between two very large numbers, each with 385,713 digits. Imagine writing those numbers down!

The largest "merit" value ever found (as of September 2022) is 41.93878373. This was found by a computer network called Gapcoin. The prime number involved has 87 digits, and the gap to the next prime is 8350.

Record-Breaking Gaps

Here's a table showing some of the largest "merit" values found:

Largest known merit values (as of October 2020)
Merit	g_n (Gap Size)	Digits in p_n	p_n (First Prime)	Date	Discoverer
41.938784	8350	87	see above	2017	Gapcoin
39.620154	15900	175	3483347771 × 409#/30 − 7016	2017	Dana Jacobsen
38.066960	18306	209	650094367 × 491#/2310 − 8936	2017	Dana Jacobsen
38.047893	35308	404	100054841 × 953#/210 − 9670	2020	Seth Troisi
37.824126	8382	97	512950801 × 229#/5610 − 4138	2018	Dana Jacobsen

Maximal Gaps

A "maximal gap" is a prime gap that is larger than all the prime gaps before it. It's like finding a new record for the longest jump. As of May 2024, the largest known maximal prime gap has a length of 1572. It was found by Craig Loizides and occurs after a very large prime number: 18,571,673,432,051,830,099.

Here is a list of the 82 known maximal prime gaps:

The 82 known maximal prime gaps

Number 1 to 27
#	g_n	p_n	n
1	1	2	1
2	2	3	2
3	4	7	4
4	6	23	9
5	8	89	24
6	14	113	30
7	18	523	99
8	20	887	154
9	22	1,129	189
10	34	1,327	217
11	36	9,551	1,183
12	44	15,683	1,831
13	52	19,609	2,225
14	72	31,397	3,385
15	86	155,921	14,357
16	96	360,653	30,802
17	112	370,261	31,545
18	114	492,113	40,933
19	118	1,349,533	103,520
20	132	1,357,201	104,071
21	148	2,010,733	149,689
22	154	4,652,353	325,852
23	180	17,051,707	1,094,421
24	210	20,831,323	1,319,945
25	220	47,326,693	2,850,174
26	222	122,164,747	6,957,876
27	234	189,695,659	10,539,432

Number 28 to 54
#	g_n	p_n	n
28	248	191,912,783	10,655,462
29	250	387,096,133	20,684,332
30	282	436,273,009	23,163,298
31	288	1,294,268,491	64,955,634
32	292	1,453,168,141	72,507,380
33	320	2,300,942,549	112,228,683
34	336	3,842,610,773	182,837,804
35	354	4,302,407,359	203,615,628
36	382	10,726,904,659	486,570,087
37	384	20,678,048,297	910,774,004
38	394	22,367,084,959	981,765,347
39	456	25,056,082,087	1,094,330,259
40	464	42,652,618,343	1,820,471,368
41	468	127,976,334,671	5,217,031,687
42	474	182,226,896,239	7,322,882,472
43	486	241,160,624,143	9,583,057,667
44	490	297,501,075,799	11,723,859,927
45	500	303,371,455,241	11,945,986,786
46	514	304,599,508,537	11,992,433,550
47	516	416,608,695,821	16,202,238,656
48	532	461,690,510,011	17,883,926,781
49	534	614,487,453,523	23,541,455,083
50	540	738,832,927,927	28,106,444,830
51	582	1,346,294,310,749	50,070,452,577
52	588	1,408,695,493,609	52,302,956,123
53	602	1,968,188,556,461	72,178,455,400
54	652	2,614,941,710,599	94,906,079,600

Number 55 to 82
#	g_n	p_n	n
55	674	7,177,162,611,713	251,265,078,335
56	716	13,829,048,559,701	473,258,870,471
57	766	19,581,334,192,423	662,221,289,043
58	778	42,842,283,925,351	1,411,461,642,343
59	804	90,874,329,411,493	2,921,439,731,020
60	806	171,231,342,420,521	5,394,763,455,325
61	906	218,209,405,436,543	6,822,667,965,940
62	916	1,189,459,969,825,483	35,315,870,460,455
63	924	1,686,994,940,955,803	49,573,167,413,483
64	1,132	1,693,182,318,746,371	49,749,629,143,526
65	1,184	43,841,547,845,541,059	1,175,661,926,421,598
66	1,198	55,350,776,431,903,243	1,475,067,052,906,945
67	1,220	80,873,624,627,234,849	2,133,658,100,875,638
68	1,224	203,986,478,517,455,989	5,253,374,014,230,870
69	1,248	218,034,721,194,214,273	5,605,544,222,945,291
70	1,272	305,405,826,521,087,869	7,784,313,111,002,702
71	1,328	352,521,223,451,364,323	8,952,449,214,971,382
72	1,356	401,429,925,999,153,707	10,160,960,128,667,332
73	1,370	418,032,645,936,712,127	10,570,355,884,548,334
74	1,442	804,212,830,686,677,669	20,004,097,201,301,079
75	1,476	1,425,172,824,437,699,411	34,952,141,021,660,495
76	1,488	5,733,241,593,241,196,731	135,962,332,505,694,894
77	1,510	6,787,988,999,657,777,797	160,332,893,561,542,066
78	1,526	15,570,628,755,536,096,243	360,701,908,268,316,580
79	1,530	17,678,654,157,568,189,057	408,333,670,434,942,092
80	1,550	18,361,375,334,787,046,697	423,731,791,997,205,041
81	1,552	18,470,057,946,260,698,231	426,181,820,436,140,029
82	1,572	18,571,673,432,051,830,099	428,472,240,920,394,477

Big Ideas and Unsolved Puzzles

Mathematicians are always trying to figure out more about prime gaps. They use complex math to set "bounds" on how big or small these gaps can be.

How Big Can Gaps Be?

Bertrand's postulate (proven in 1852) says there's always a prime number between any number k and its double, 2k. This means a prime gap can never be as big as the prime number itself.
The prime number theorem suggests that as primes get bigger, the average gap between them grows slowly.
More recently, in 2013, a mathematician named Yitang Zhang made a huge breakthrough. He proved that there are infinitely many prime gaps that are smaller than 70 million. This means that even very far out on the number line, you'll keep finding primes that are relatively close together. Other mathematicians then worked together to lower this number even further, down to 246! This is a big step towards solving the twin prime conjecture.

How Small Can Gaps Be?

In 1931, Erik Westzynthius showed that prime gaps can grow faster than the logarithm of the prime numbers. This means that even though the average gap increases, there will always be some gaps that are much, much larger than average.
Mathematicians have also proven that there are infinitely many prime gaps that are very large, growing in a specific way.

Conjectures: What Mathematicians Believe (But Can't Prove Yet)

Many ideas about prime gaps are still just conjectures. These are statements that mathematicians strongly believe are true, but they haven't found a complete proof for them yet.

Prime gap function

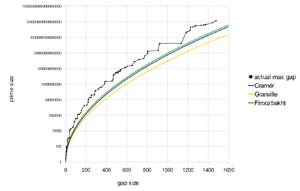
Cramér's Conjecture: This idea suggests that prime gaps are usually quite small. It says that the gap g_n is roughly proportional to the square of the natural logarithm of the prime number.
Firoozbakht's Conjecture: This is another idea that suggests prime gaps get smaller relative to the primes as the numbers get larger. If this is true, it would mean Cramér's conjecture is also true in a strong way.
Oppermann's Conjecture: This is a slightly less strict idea than Cramér's. It suggests that prime gaps are usually smaller than the square root of the prime number.
Andrica's Conjecture: This is even weaker than Oppermann's. It says that the gap g_n is always less than twice the square root of the prime number plus one. This is related to the idea that there's always a prime between any two consecutive square numbers.
Polignac's Conjecture: This is a very interesting idea. It says that every even number k appears as a prime gap infinitely often. For example, it suggests there are infinitely many gaps of size 2 (the twin prime conjecture), infinitely many gaps of size 4, infinitely many gaps of size 6, and so on. While not proven for any specific k, the recent breakthroughs by Yitang Zhang and others show that it's true for at least one even number less than or equal to 246!