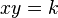Proportionality (mathematics) facts for kids

The variable y is directly proportional to the variable x with a constant of proportionality around 0.6.

The variable y is inversely proportional to the variable x with a constant of proportionality of 1.

In mathematics, two things are proportional if they change together in a steady way. This means their relationship follows a clear rule. There are two main types: direct proportionality and inverse proportionality.

When two things are directly proportional, if one increases, the other increases by the same factor. If one decreases, the other decreases by the same factor. Think of it like this: if you buy twice as many apples, you pay twice as much money. The constant number that connects them is called the constant of proportionality.

When two things are inversely proportional, if one increases, the other decreases. And if one decreases, the other increases. But their product (when you multiply them) always stays the same. For example, if you drive twice as fast, it takes you half the time to get somewhere.

Proportionality helps us understand how different amounts are related in the real world.

What is Direct Proportionality?

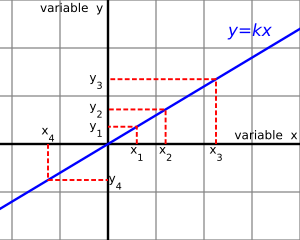
When we say y is directly proportional to x, it means that y is always a certain number times x. We can write this as a simple equation:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y = kx

Here, k is the constant of proportionality. It's a number that never changes for that specific relationship.

You might also see this relationship shown with special symbols:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y \propto x

or

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y \sim x

If you know y and x, you can find the constant k by dividing y by x:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): k = \frac{y}{x}

This means that for any pair of x and y values that are directly proportional, the result of y divided by x will always be the same number, k.

Everyday Examples

• Distance and Time: If you drive at a steady speed, the longer you drive, the farther you go. The distance you travel is directly proportional to the time you spend driving. Your speed is the constant of proportionality.
• Circle Size: The distance around a circle (its circumference) is directly proportional to the distance across it (its diameter). The constant of proportionality here is the famous number π (about 3.14).
• Maps: On a map, the distance between two points on the map is directly proportional to the real-life distance between those places. The map's scale is the constant of proportionality.
• Gravity: The force of gravity pulling on an object is directly proportional to its mass. A heavier object feels a stronger pull. The constant of proportionality is called gravitational acceleration.

What is Inverse Proportionality?

This graph shows inverse proportionality. As x gets bigger, y gets smaller, but their product stays the same.

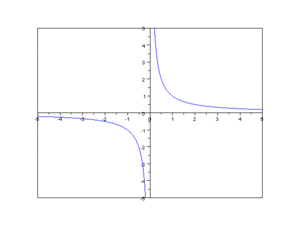
Inverse proportionality is the opposite of direct proportionality. When two things are inversely proportional, one goes up while the other goes down. But there's a special rule: their product (when you multiply them together) always stays the same.

We can write this relationship as:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y = \frac{k}{x}

Or, if you multiply both sides by x, you get:

Here, k is still the constant of proportionality, but this time it's the product of x and y.

An Example

• Travel Time and Speed: Imagine you need to travel a certain distance. If you increase your speed, the time it takes to get there will decrease. If you drive twice as fast, it will take you half the time. The time taken for a journey is inversely proportional to your speed. The constant k in this case would be the total distance you travel.

How Proportionality Looks on a Graph

• Direct Proportionality: If you plot directly proportional values on a graph, they will form a straight line that goes through the point (0,0) (the origin).
• Inverse Proportionality: If you plot inversely proportional values on a graph, they will form a curved line called a rectangular hyperbola. This curve never touches the x or y axes.

Computer Symbols for Proportionality

Computers use special symbols to show proportionality:

• ∝ (proportional to)
• ~ (tilde, also used for proportional to)

See also

• Linear map
• Correlation
• Ratio
• Rule of three (mathematics)
• Similarity