Riemann sum facts for kids

This picture shows four ways to estimate the area under a curve using Riemann sums. The right and left methods use the right or left side of each small section. The maximum and minimum methods use the highest or lowest point in each section. As the sections get smaller, the estimates get closer to the real area.

In mathematics, a Riemann sum is a special way to guess the total area under a curved line on a graph. This area is also called an integral. Riemann sums can also help us understand how to find this area. The idea is named after a German mathematician named Bernhard Riemann.

How Riemann Sums Work

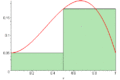
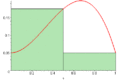
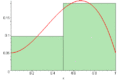
Imagine you want to find the area under a curved line. It's hard to measure a curved shape directly. Riemann sums help by breaking the area into many small, simple shapes, usually rectangles.

First, you pick a section of the graph you want to measure. Then, you divide this section into many narrow, equal parts. Each part becomes the width of a rectangle.

Next, for each narrow part, you draw a rectangle. The height of this rectangle is chosen based on the curve. For example, you might use the height of the curve at the left side of the narrow part, or the right side, or even the middle.

The area of one rectangle is its width multiplied by its height. Since you have many small rectangles, you find the area of each one.

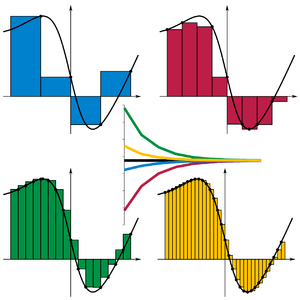
Finally, you add up the areas of all these small rectangles. This total sum is your guess, or approximation, for the total area under the curved line. The more rectangles you use, and the narrower they are, the closer your guess will be to the real area.

Different Ways to Sum

There are a few common ways to choose the height of each rectangle:

• Left Riemann Sum: You use the height of the curve at the left edge of each narrow section.
• Right Riemann Sum: You use the height of the curve at the right edge of each narrow section.
• Midpoint Riemann Sum: You use the height of the curve at the very middle of each narrow section. This often gives a very good estimate.

No matter which method you use, the goal is always the same: to add up the areas of many small rectangles to estimate the area under a curve.

Images for kids

• 

  This shows a Left Riemann Sum. The height of each rectangle is set by the left side of its base.

• 

  This shows a Right Riemann Sum. The height of each rectangle is set by the right side of its base.

• 

  This shows a Midpoint Riemann Sum. The height of each rectangle is set by the middle point of its base.

See also

In Spanish: Suma de Riemann para niños