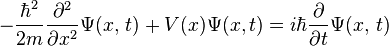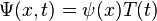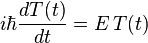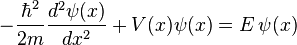Schrödinger equation Facts for Kids

Schrödinger's equation is carved on the gravestone of Erwin Schrödinger.

The Schrödinger equation is a special kind of equation used in quantum mechanics. Quantum mechanics is a science that helps us understand how super tiny things, like subatomic particles, behave. This equation was created by Erwin Schrödinger in 1925.

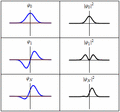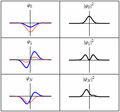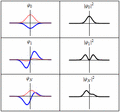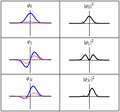
It uses something called a wave function (written as 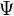$\Psi$ ). This wave function is like a map that describes a particle or a group of particles. It tells us where a particle might be at any given time. The numbers in the wave function are complex, so they don't have a direct physical meaning on their own. However, this wave function holds all the information we can know about a particle. By doing some math with it, we can figure out real things like a particle's position, how fast it's moving (its momentum), or its energy. Think of the wave function as a complete picture of how a particle acts over time.

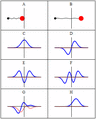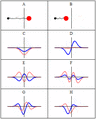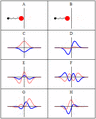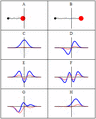
A particle's wave function can be in many different states at once. This means a tiny particle could seem to be in many places or have many energies at the same time. This is often called "being in two places at once." But when we actually measure one of these properties, the particle suddenly picks just one specific value. This is called wave function collapse. Scientists are still discussing why this happens and what it truly means.

For a single particle moving in one direction, the Schrödinger equation looks like this:

$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\Psi(x,\,t) + V(x)\Psi(x,t) = i\hbar\frac{\partial}{\partial t} \Psi(x,\,t)$

In this equation:

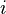$i$ is a special number (the square root of -1).
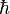$\hbar$ is the reduced Planck constant, a very small number important in quantum physics.
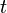$t$ stands for time.
$x$ stands for position.
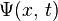$\Psi(x,\,t)$ is the wave function we talked about.
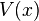$V(x)$ is the potential energy, which changes depending on the particle's position.

Time-Independent Schrödinger Equation

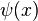Sometimes, we look at systems where the energy of the particle stays the same over time. For these situations, the Schrödinger equation can be simplified. We can separate the wave function $\Psi (x,t)$ into two parts: one that depends only on position ( $\psi (x)$ ) and one that depends only on time ( $T(t)$ ).

$\Psi (x,t) = \psi (x) T(t)$

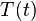When we do this, the main equation splits into two simpler equations:

$i\hbar \frac{d T(t)}{dt} = E \, T(t)$

$-\frac{\hbar^2}{2m} \frac{d^2 \psi (x)}{dx^2}+V(x) \psi (x) = E \, \psi (x)$

The first equation tells us how the time part of the wave function changes. The second equation, which only depends on position, is called the Time-Independent Schrödinger Equation. The letter 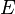$E$ in these equations represents the total energy of the system.

This time-independent version is very useful because the energy of many important physical systems, like an electron moving around an atom, stays constant.

Images for kids

A wave function for a particle moving freely in empty space.
These images show wave functions for a quantum harmonic oscillator. The left side shows the wave function itself, and the right side shows where the particle is most likely to be found. The top two rows are "stationary states," meaning their probability doesn't change over time.
This compares a simple back-and-forth motion (like a ball on a spring) in classical physics (A–B) with how it looks in quantum mechanics (C–H) using the Schrödinger equation.
Erwin Schrödinger, the scientist who created the equation.

Schrödinger equation facts for kids

Time-Independent Schrödinger Equation

Images for kids

See also