Semi-symmetric graph facts for kids

A semi-symmetric graph is a special kind of drawing or network in the area of mathematics called graph theory. Imagine a drawing made of dots (called vertices) and lines (called edges) connecting them.

A graph is semi-symmetric if it has these three important features:

• Regular: Every dot has the exact same number of lines connected to it.
• Edge-transitive: You can flip, spin, or move the graph in a way that makes any line land exactly where any other line was. It means all lines look "the same" in terms of the graph's overall shape.
• Not vertex-transitive: Even though the lines might look the same, you can't always flip or spin the graph so that *any* dot lands exactly where *any other* dot was. Some dots are unique, even if they have the same number of lines connected to them.

The Folkman graph, the smallest semi-symmetric graph.

What Makes Them Special?

Semi-symmetric graphs are always bipartite. This means you can color all the dots with two colors (like red and green) so that no two dots of the same color are connected by a line.

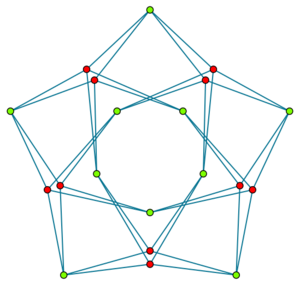
In a semi-symmetric graph, even though you can't move *any* dot to *any other* dot using symmetries, you *can* move any red dot to any other red dot, and any green dot to any other green dot. Look at the Folkman graph picture: you can't swap a green dot for a red one using a symmetry, but all green dots are "alike" to each other, and all red dots are "alike" to each other.

How They Were Discovered

The idea of semi-symmetric graphs was first looked at by a student named E. Dauber. Later, in 1967, a mathematician named Jon Folkman published a paper that included the smallest semi-symmetric graph. This graph has 20 dots and is now known as the Folkman graph.

The actual name "semi-symmetric" was first used in 1978 by Klin and his team.

Cubic Semi-Symmetric Graphs

A cubic graph is a graph where every single dot has exactly three lines connected to it.

The smallest cubic semi-symmetric graph is called the Gray graph. It has 54 dots. It was first noticed to be semi-symmetric in 1968. Later, mathematicians Dragan Marušič and Aleksander Malnič proved that it truly is the smallest one.

Scientists have found all the cubic semi-symmetric graphs that have up to 768 dots. Some of the next smallest ones after the Gray graph include:

• The Iofinova–Ivanov graph (110 dots)
• The Ljubljana graph (112 dots)
• A graph with 120 dots that has a "girth" of 8 (meaning its shortest loop has 8 lines)
• The Tutte 12-cage