Gray graph facts for kids
Quick facts for kids Gray graph |
|
|---|---|

The Gray graph
|
|
| Named after | Marion Cameron Gray |
| Vertices | 54 |
| Edges | 81 |
| Radius | 6 |
| Diameter | 6 |
| Girth | 8 |
| Automorphisms | 1296 |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Cubic Semi-symmetric Hamiltonian Bipartite |
| Table of graphs and parameters | |
The Gray graph is a special kind of graph in mathematics. Think of a graph as a network of dots (called vertices) connected by lines (called edges). The Gray graph has 54 vertices and 81 edges. It's also a cubic graph, which means every single dot (vertex) is connected to exactly three lines (edges).
This interesting graph was first found by Marion Cameron Gray in 1932, though her work wasn't published then. Later, in 1968, another mathematician named Bouwer discovered it again on his own. The Gray graph is important because it was the first known example of a cubic graph that has a special property: its edges can be moved around by symmetries, but its vertices cannot.
The Gray graph has a chromatic number of 2. This means you only need two colors to color its vertices so that no two connected vertices have the same color. Its chromatic index is 3, meaning you need three colors for its edges. It also has a radius and diameter of 6, which are ways to measure how "spread out" the graph is.
How the Gray Graph is Built
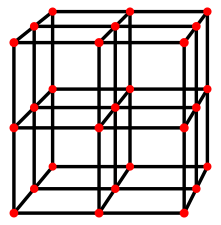
Imagine a giant cube made of 27 points, arranged in a 3x3x3 grid, like a Rubik's Cube. Now, imagine all the lines that go straight through these points, parallel to the sides of the cube. There are 27 such lines.
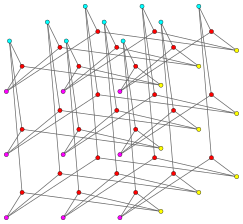
The Gray graph is built from these points and lines. It has a vertex for every point and a vertex for every line. An edge connects a point-vertex to a line-vertex if that point is on that line. This way of building a graph is called a Levi graph. Because it's built this way, the Gray graph is a bipartite graph. This means its vertices can be split into two groups (points and lines), and edges only connect vertices from different groups, never from the same group.
Mathematicians have found other ways to build the Gray graph too. It's known that the Gray graph has no cycles (closed paths) of length 4 or 6. Its shortest cycle is 8 vertices long, which is called its girth.
The Gray graph is also a Hamiltonian graph. This means you can draw a path that visits every single vertex exactly once and ends where it started.
Special Symmetries of the Gray Graph
The Gray graph has many symmetries. Its full group of symmetries, called its automorphism group, has 1296 different ways to transform the graph onto itself while keeping its structure.
What's really special about the Gray graph is how these symmetries work. You can rotate or flip the graph in a way that moves any edge to any other edge. This is called being "edge-transitive." However, you cannot do the same for its vertices. You can't always move any vertex to any other vertex using a symmetry. For example, a vertex that represents a "point" in our 3x3x3 grid can only be moved to another "point" vertex, not to a "line" vertex.
Because of this, the Gray graph is called a semi-symmetric graph. It's the smallest possible cubic graph that has this interesting "edge-transitive but not vertex-transitive" property.