Cubic graph facts for kids
In mathematics, especially in a field called graph theory, a cubic graph is a special kind of graph. Imagine a graph as a network of dots (called vertices) connected by lines (called edges). In a cubic graph, every single dot has exactly three lines connected to it. This is why they are also called 3-regular graphs or trivalent graphs.
A bicubic graph is a cubic graph that is also a bipartite graph. A bipartite graph is one where you can split the dots into two groups, and all the lines only connect dots from one group to dots in the other group, never within the same group.
Contents
Symmetry in Cubic Graphs
Some cubic graphs are very balanced and look the same even if you turn them around or flip them. This is called being symmetric. In 1932, a person named Ronald M. Foster started collecting examples of these symmetric cubic graphs. His collection is now known as the Foster census.
Many famous graphs are both cubic and symmetric. These include the Petersen graph, the Heawood graph, the Pappus graph, and the Desargues graph. Some cubic graphs are semi-symmetric, meaning they are symmetric in some ways but not completely. The Gray graph is the smallest example of a semi-symmetric cubic graph.
Not all cubic graphs are symmetric. The Frucht graph is one of the smallest cubic graphs that has almost no symmetry at all. It only looks the same if you don't move it.
Coloring Cubic Graphs
Imagine you want to color the dots or lines of a graph. In graph theory, this is called "graph coloring."
Coloring Vertices
According to Brooks' theorem, most connected cubic graphs can have their dots colored with just three different colors. The only exception is a very small graph called K4, which has four dots and all of them are connected to each other. If you color a graph with three colors, you can always find a group of dots that are not connected to each other, and this group will have at least one-third of all the dots in the graph.
Coloring Edges
You can also color the lines (edges) of a graph. According to Vizing's theorem, every cubic graph needs either three or four colors for its edges. When a cubic graph can be colored with exactly three edge colors, it's called a Tait coloring. This means you can split all the lines into three perfect groups, where no two lines in the same group touch the same dot. All bicubic graphs (the ones that are both cubic and bipartite) can have a Tait coloring.
What are Snarks?
Some cubic graphs cannot be colored with only three edge colors, even if they don't have any "bridges" (a bridge is an edge that, if removed, would split the graph into two separate parts). These special graphs are called snarks. The Petersen graph is a famous example of a snark. There are many, many different snarks, an endless number of them!
Finding Paths in Cubic Graphs
A big question in graph theory is about finding special paths in graphs called Hamiltonian circuits. A Hamiltonian circuit is a path that visits every dot in the graph exactly once and then returns to the starting dot.
In 1880, P.G. Tait thought that every cubic graph that could be drawn without lines crossing (like the edges of a polyhedron) would have a Hamiltonian circuit. But in 1946, William Thomas Tutte found a graph, the Tutte graph, that proved Tait wrong. It was a cubic graph that could be drawn without crossings, but it didn't have a Hamiltonian circuit.
Later, Tutte himself thought that all bicubic graphs (cubic and bipartite) would have a Hamiltonian circuit. But again, a counterexample was found by Joseph Horton, called the Horton graph.
Even though finding Hamiltonian circuits can be tricky, if you pick a cubic graph randomly, it's very likely to have a Hamiltonian circuit, especially as the graph gets bigger. Scientists have also studied how many different Hamiltonian circuits a cubic graph can have.
Other Interesting Facts
It's a cool fact, proven by Leonhard Euler way back in 1736, that every cubic graph must have an even number of dots (vertices). You can't have a cubic graph with an odd number of dots!
Another important idea is Petersen's theorem, which says that every cubic graph without bridges (edges that would split the graph if removed) has something called a perfect matching. A perfect matching is a set of edges where every dot in the graph is connected to exactly one edge in that set.
Scientists have also found that cubic graphs without bridges have a huge number of perfect matchings. For a graph with n dots, there are at least 2n/3656 perfect matchings, which is a very large number!
Images for kids
See also
 In Spanish: Grafo cúbico para niños
In Spanish: Grafo cúbico para niños



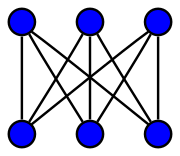
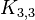 is an example of a bicubic graph
is an example of a bicubic graph