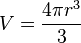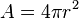Sphere facts for kids
A sphere is a special 3D shape. It looks exactly like the outside of a ball. Think of a basketball or a playground ball. In everyday talk, we often use "ball" and "sphere" to mean the same thing.
But in mathematics, a sphere has a very exact definition. It's made up of all the points in 3D space that are the same distance from a central point. This fixed distance is called the radius of the sphere.
A sphere is like a circle, but in three dimensions instead of two.
Contents
How to Find the Volume of a Sphere
The volume of a sphere tells you how much space it takes up. Imagine how much air you could fit inside a basketball. That's its volume!
You can find the volume (V) using this formula:
Here, r stands for the radius of the sphere. The radius is the distance from the very center of the sphere to any point on its surface.
How to Find the Surface Area of a Sphere
The surface area of a sphere is the total area of its outer skin. Think about how much material you would need to cover a ball completely. That's its surface area!
You can find the surface area (A) using this formula:
Again, r stands for the radius of the sphere.
Images for kids
-
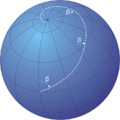
A Great circle on a sphere. This is the largest circle you can draw on a sphere.
-
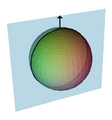
This is one of the most perfect spheres ever made by people! It was part of an experiment called Gravity Probe B. It's so smooth that it's almost perfectly round, differing by less than the thickness of 40 atoms. You can even see Albert Einstein's image reflected in it!
See also
 In Spanish: Esfera para niños
In Spanish: Esfera para niños