Tennis racket theorem facts for kids
The tennis racket theorem is a cool idea in classical mechanics. It explains how a solid object spins when it has three different ways it likes to turn. You might also hear it called the intermediate axis theorem.
It's also known as the Dzhanibekov effect. This name comes from a Russian cosmonaut named Vladimir Dzhanibekov. He noticed this effect in space in 1985. Even though he saw it, scientists had known about this spinning trick for over 150 years before him!
The theorem says that if an object spins around its "first" or "third" main turning lines (called principal axes), it will spin steadily. But if it tries to spin around its "second" or "middle" main turning line, it will wobble and flip over.
The Tennis Racket Trick
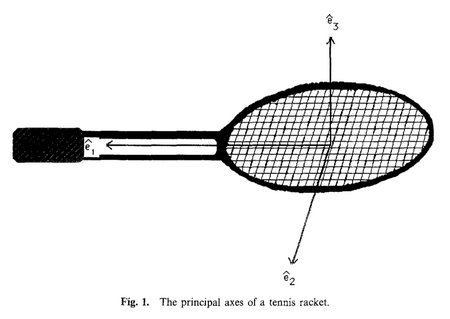
You can see this effect with a tennis racket. Hold the racket by its handle, with the flat part facing up. Now, try to throw it into the air so it spins once around the horizontal line that goes across the racket's face. Try to catch the handle again.
What usually happens? As the racket spins, its face will often flip over! So, the other side of the racket will be facing up when you catch it. This is the tennis racket theorem in action.
Now, try spinning the racket in other ways.
- It's easy to spin the racket around its handle (the long way). It won't flip.
- It's also easy to spin it around the vertical line that goes through the handle. It won't flip either.
The "flip" only happens when you try to spin it around that tricky middle axis.
You can try this experiment with other things too! Any object that has three different "weights" for spinning will work. A book, a TV remote, or even a smartphone can show this effect. This flipping happens even if there's no air or gravity. It's all about how the object is shaped and how its weight is spread out.
Why Does This Happen?
Every object has special lines, or "axes," it can spin around. Think of these as imaginary lines going through the object. For the tennis racket theorem, we look at three main axes. Each axis has a different "moment of inertia." This is like how hard or easy it is to make an object spin around that particular line.
- One axis is the "easiest" to spin around (smallest moment of inertia).
- Another axis is the "hardest" to spin around (largest moment of inertia).
- And then there's the "middle" axis.
The theorem tells us that spinning around the easiest axis is stable. Spinning around the hardest axis is also stable. But spinning around that middle axis is unstable. Even a tiny little nudge can make the object wobble and flip its direction. It's like trying to balance something perfectly on a very thin edge – it's just not stable!
This effect is a basic rule of how things move and spin in the universe. It shows us that not all spins are created equal!
Images for kids
-
A visualization of the instability of the intermediate axis.
See also
In Spanish: Teorema del eje intermedio para niños
