Three utilities problem facts for kids

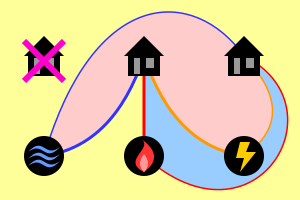
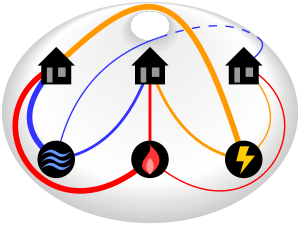
The classical mathematical puzzle known as the three utilities problem is a fun brain teaser! It's also called the three cottages problem or sometimes water, gas and electricity. Imagine you have three houses and three utility companies: water, gas, and electricity. Your challenge is to connect each house to each of the three utility companies. The tricky part? You can't let any of the connection lines cross each other!

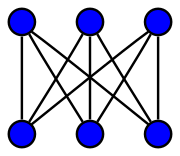
This puzzle is an abstract math problem. It sets up rules that wouldn't apply in real-life engineering. It's part of a branch of math called topological graph theory, which studies how shapes (called graphs) can be drawn on different surfaces. In math terms, the puzzle asks if a special kind of graph, called K_3,3, can be drawn flat without lines crossing. This graph is often called the utility graph because of this puzzle.

Solving the Puzzle: Is it Possible?

The utility graph, also known as the Thomsen graph or K_3,3. It shows the three houses connected to the three utilities.

Proof without words: This picture helps explain why the puzzle is impossible on a flat surface. If you try to connect all the houses and utilities, you'll always end up with lines crossing.

When the puzzle is presented on a flat surface, like a piece of paper, the answer is "no." There's no way to connect all nine lines (three houses x three utilities) without some lines crossing.

In other words, the K_3,3 graph cannot be drawn flat without crossings. A mathematician named Kazimierz Kuratowski stated in 1930 that this graph is "nonplanar," meaning it can't be drawn on a flat plane without lines crossing. This means the puzzle has no solution on a flat surface.

Mathematicians have different ways to prove this. One way involves looking at how the lines would divide the flat surface and showing that it's impossible to connect everything without a line having to cross another. Another way uses a special math formula called the Euler formula, which helps describe shapes drawn on a flat surface. This formula shows that the utility graph simply doesn't fit the rules for graphs that can be drawn without crossings.

Changing the Rules: When it Becomes Possible

The K_3,3 graph can be drawn with just one crossing if you try to make it as neat as possible.

Even though the puzzle is impossible on a flat surface, it becomes possible if you change the rules a little!

Solving on a Different Surface

Solution to the three utilities problem on a torus. Notice how the lines go around the "donut" shape without crossing.

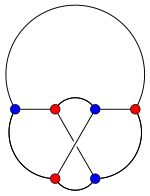
Imagine the puzzle isn't on a flat piece of paper, but on the surface of a donut! A donut shape is called a torus in math. The K_3,3 graph can be drawn without any crossings on a torus.

Think of it like this: if you punch two holes through a flat surface and connect them with a tube, you've created a torus. By using this "tube," you can guide the utility lines so they don't cross. This changes the "shape" of the surface you're drawing on, making the puzzle solvable.

Other Ways to Solve It

Another way to solve the puzzle is to change the rules about how the lines can be drawn. For example, if you were allowed to let utility lines pass through the houses or other utility companies, the puzzle would also become solvable. This extra freedom makes it much easier to connect everything without crossings.

Mathematicians also study how many crossings are absolutely necessary if you *have* to draw the graph on a flat surface. For the utility graph K_3,3, the smallest number of crossings you need is just one. You can't draw it with zero crossings, but you can draw it with only one.

Other Cool Math Facts

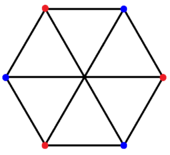
The utility graph K_3,3 has some other interesting properties in graph theory. For example, it's a "circulant graph," which means its connections follow a repeating pattern. It's also the smallest "triangle-free" graph that is "cubic" (meaning every point has exactly three lines connected to it).

This puzzle is a great example of how math can be used to understand shapes and connections, even in abstract ways!

• Eric W. Weisstein, Utility graph at MathWorld.

See also

In Spanish: Problema de los tres servicios para niños