Travelling salesman problem facts for kids

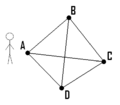
The Traveling Salesman Problem (often called TSP) is a famous puzzle in computer science. It's all about finding the best way to do something. "Best" usually means the cheapest, shortest, or fastest way. TSP is a math problem that uses a graph. A graph shows locations (called nodes) and the paths between them.

Who Invented the Traveling Salesman Problem?

The Traveling Salesman Problem was first described in the 1800s. Two mathematicians, W. R. Hamilton from Ireland and Thomas Kirkman from Britain, helped define it. Later, in the 1930s, mathematicians like Karl Menger in Vienna and at Harvard studied it more.

Menger described it as the "messenger problem." He wondered how a postman could find the shortest route to visit many points. He also noticed that simply going to the closest point each time might not give the shortest overall route. The name "Traveling Salesman Problem" was later introduced by Hassler Whitney at Princeton University.

What is the Traveling Salesman Problem?

Imagine a salesman who needs to visit many cities. He wants to visit each city only once. After visiting all cities, he needs to return to his starting point.

Each city is connected to others by airplanes, roads, or railways. These connections have a "cost." This cost could be the price of a ticket, the distance between cities, or the time it takes to travel. The salesman wants to find a route where the total cost and total distance are as low as possible.

This problem is important in real life. For example, when making a circuit board, a laser needs to drill thousands of holes. Finding the best order for the laser to drill these holes is like solving a TSP. An efficient solution helps reduce how much it costs to make things.

Why is the Traveling Salesman Problem Hard to Solve?

The Traveling Salesman Problem is known as an "NP-hard" problem. This means it's very difficult to solve perfectly, especially as the number of cities grows. It's hard because you can't easily break it into smaller, simpler parts.

The easiest way to solve it is to try every single possible route. But this quickly becomes impossible! If you have N cities, there are (N-1) factorial possible routes.

Let's look at an example:

• For only 10 cities, there are over 180,000 different routes to try!
• This is because the starting city is fixed. Then you can arrange the remaining nine cities in many ways.
• We divide by two because going A-B-C-D is the same length as D-C-B-A.
• So, 9! / 2 = 181,440 possible routes.

Trying every route takes too much time, even for powerful computers, if there are many cities.

How Do We Find Solutions?

Since trying every route is too hard, computer scientists use different methods:

• Exact Solutions: These methods, like "branch and bound" algorithms, can find the absolute best solution. They work by cleverly ruling out bad routes without checking them all. Currently, they can solve problems with up to 85,900 cities.

• Heuristic Solutions: These are like "good guesses" or "rules of thumb." They don't always find the perfect solution, but they find a very good one much faster. A heuristic might tell the salesman to visit cities that are close together first. This helps find a useful route quickly, even if it's not the absolute shortest. Examples include Monte Carlo algorithms.

Images for kids

• 

  A salesman wants to visit all cities, A, B, C, and D. What is the best way to do this (cheapest airline tickets, and minimal travel time)?

• 

  The shortest route for a salesman visiting 15 big cities in Germany. This is the shortest of over 43 billion possible routes.

• 

  William Rowan Hamilton

• 

  Solution to a symmetric TSP with 7 cities using brute force search. Note: Number of permutations: (7−1)!/2 = 360

• 

  Solution of a TSP with 7 cities using a simple Branch and bound algorithm. Note: The number of permutations is much less than Brute force search

• 

  Nearest Neighbour algorithm for a TSP with 7 cities. The solution changes as the starting point is changed

• 

  Creating a matching

• 

  An example of a 2-opt iteration

See also

In Spanish: Problema del viajante para niños