Verbal arithmetic Facts for Kids

Verbal arithmetic, also known as alphametics or cryptarithmetic, is a fun mathematical game. In these puzzles, letters stand for unknown numbers. Your goal is to figure out which number each letter represents.

These puzzles usually involve basic math like addition or multiplication. A famous example, from 1924, is: 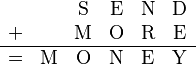$\begin{matrix} & & \text{S} & \text{E} & \text{N} & \text{D} \\ + & & \text{M} & \text{O} & \text{R} & \text{E} \\ \hline = & \text{M} & \text{O} & \text{N} & \text{E} & \text{Y} \\ \end{matrix}$ The answer to this puzzle is: O = 0, M = 1, Y = 2, E = 5, N = 6, D = 7, R = 8, and S = 9.

In these puzzles, each letter must stand for a different number. Also, numbers with more than one digit cannot start with zero. A good puzzle has only one correct answer. Often, the letters spell out meaningful words or phrases, like "SEND MORE MONEY."

Verbal arithmetic can be a great way to learn and practice algebra skills.

History of Cryptarithms
Types of Cryptarithms
How to Solve Cryptarithms
See also

History of Cryptarithms

These number puzzles are quite old. No one knows who invented them. An example from 1864 shows they were around long before some people thought.

The name "cryptarithm" was first used by a puzzle maker named Minos in 1931. Later, in 1955, J. A. H. Hunter created the word "alphametic." This word is used for cryptarithms where the letters form real words, like the "SEND MORE MONEY" puzzle.

Types of Cryptarithms

There are different kinds of cryptarithms. The main types are alphametics, digimetics, and skeletal divisions.

Alphametic Puzzles

An alphametic is a puzzle where words are set up like a math problem, often an addition sum. You need to replace each letter with a number from 0 to 9. The goal is to make the math problem correct.

Digimetic Puzzles

In a digimetic, digits are used to stand for other digits. It's like a code where one number replaces another.

Skeletal Division Puzzles

This type of puzzle is a long division problem. Most or all of the numbers are replaced by symbols, usually asterisks (*). You have to figure out the missing numbers.

How to Solve Cryptarithms

Solving a cryptarithm by hand means using logic and trying out different numbers. Let's look at how to solve the famous SEND+MORE = MONEY puzzle step-by-step.

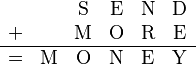
$\begin{matrix} & & \text{S} & \text{E} & \text{N} & \text{D} \\ + & & \text{M} & \text{O} & \text{R} & \text{E} \\ \hline = & \text{M} & \text{O} & \text{N} & \text{E} & \text{Y} \\ \end{matrix}$

Step 1: Find M. Look at the leftmost column (column 5). When you add two single-digit numbers, the biggest possible carry-over is 1. So, M must be 1.
Step 2: Find O. Since there's a carry-over to M (which is 1), O must be less than M. O cannot be the same as M. So, O must be 0.
Step 3: Find S. In column 4, S + M (which is 1) results in MO. Since O is 0, S + 1 must be 10 or more to carry over to M. If there was a carry from column 3, S + 1 + carry = MO. But if N = E, that's impossible. So, there is no carry from column 3. This means S must be 9.
Step 4: Find N and E (first part). If there was no carry from column 3, then E would equal N. But each letter must be a different digit. So, there must be a carry from column 2 to column 3. This means N = E + 1.
Step 5: Find R. In column 2, N + R results in E, with a carry to column 3. We know N = E + 1. So, (E + 1 + R) must be 10 + E (because of the carry). This means 1 + R = 10, so R = 9. But S is already 9, and letters must be different. This means there must be a carry from column 1 to column 2. So, R must be 8.
Step 6: Find D and E (second part). In column 1, D + E results in Y, with a carry to column 2. This means D + E = 10 + Y.
Step 7: Find D and E (third part). Y must be at least 2 (since 0 and 1 are taken). So D + E must be at least 12. The numbers left to use are 2, 3, 4, 5, 6, 7. The only pairs that add up to 12 or more are (5,7) and (6,7). So either E=7 or D=7.
Step 8: Final numbers. We know N = E + 1. If E were 7, then N would be 8, but R is already 8. So E cannot be 7. This means D must be 7. If D is 7, then E cannot be 6 (because N would be 7, which is D). So, E must be 5 and N must be 6.
Step 9: Find Y. Since D = 7 and E = 5, D + E = 12. So, Y must be 2 (from D + E = 10 + Y). So, Y = 2.

Another example is TO+GO=OUT: 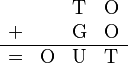$\begin{matrix} & & \text{T} & \text{O} \\ + & & \text{G} & \text{O} \\ \hline = & \text{O} & \text{U} & \text {T}\\ \end{matrix}$

Step 1: Find O. The largest sum of two two-digit numbers is 99 + 99 = 198. This means the first digit of the answer (O) must be 1. So, O = 1. There is a carry-over to the leftmost column.
Step 2: Find T. In the rightmost column, O + O = T. Since O is 1, 1 + 1 = T. So, T = 2.
Step 3: Find U and G. In the middle column, T + G = U (with a carry-over to O). We know T = 2. So, 2 + G must be 10 or more to create the carry-over. If G were 9, then 2 + 9 = 11. This would make U = 1. But O is already 1, and letters must be different. So, G cannot be 9. The only other option for G to make a carry-over is G = 8. Then 2 + 8 = 10. This means U = 0.

Computers can also solve cryptarithms. They can try every possible number combination for the letters. For the SEND+MORE=MONEY puzzle, there are over a million ways to assign numbers to the letters! Computers can also use special methods like backtracking to find the solution faster.

Verbal arithmetic facts for kids

Contents