Bayesian inference facts for kids

Bayesian inference is a clever way to update what you believe about something when you get new information or evidence. Imagine you have a guess about how likely something is to happen. When you learn new facts, Bayesian inference helps you adjust your guess to be more accurate. It uses a special math rule called Bayes' theorem.

This method is super useful in many areas, like science, engineering, medicine, sport, and even law. It's especially good for understanding how things change over time as you collect more data.

What is Bayes' Theorem?

A picture showing how Bayes' theorem works. It helps us see how the probability of something changes when we get new information.

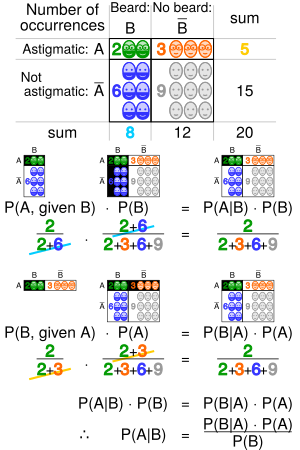
Bayes' theorem is the main tool used in Bayesian inference. It helps you figure out the new probability of a hypothesis (your idea or guess) after you've seen some evidence.

Here's the basic idea of the formula: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle P(H \mid E) = \frac{P(E \mid H) \cdot P(H)}{P(E)}}

Let's break down what each part means:

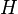• is your hypothesis (the idea you're testing).
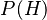• is the prior probability. This is how likely you thought your hypothesis was before you saw any new evidence.
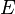• is the evidence (the new information or data you've observed).
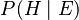• is the posterior probability. This is the new, updated probability of your hypothesis after you've considered the evidence. This is what you want to find!
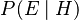• is the likelihood. This is how likely it is to see the evidence 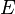if your hypothesis 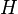is true.
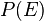• is the probability of seeing the evidence 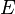at all. This part helps make sure all your probabilities add up correctly.

In simple terms, the updated probability of your idea (posterior) is based on how likely your idea was to begin with (prior) and how well the new information fits with your idea (likelihood).

A Cookie Example

Let's use a fun example to understand Bayes' theorem. Imagine you have two bowls of cookies:

• Bowl #1 has 10 chocolate chip cookies and 30 plain cookies. (Total 40)
• Bowl #2 has 20 chocolate chip cookies and 20 plain cookies. (Total 40)

Your friend Fred picks one bowl without looking, and then picks one cookie from that bowl without looking. The cookie turns out to be a plain one. What's the probability that Fred picked the cookie from Bowl #1?

Here's how we use Bayes' theorem:

• Hypothesis (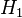): Fred picked from Bowl #1.
• Hypothesis (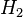): Fred picked from Bowl #2.
• Evidence (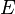): The cookie is plain.

1. Prior Probabilities: Since Fred picked a bowl at random, he had an equal chance of picking either bowl. * 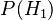(probability of picking Bowl #1) = 0.5 (or 50%) * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(H_2) (probability of picking Bowl #2) = 0.5 (or 50%)

2. Likelihoods: How likely is it to get a plain cookie from each bowl? * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(E \mid H_1) (probability of a plain cookie given Bowl #1) = 30 plain cookies / 40 total cookies = 0.75 * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P(E \mid H_2) (probability of a plain cookie given Bowl #2) = 20 plain cookies / 40 total cookies = 0.5

3. Now, let's use Bayes' theorem to find 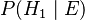(the probability that Fred picked from Bowl #1, given that the cookie was plain): Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \begin{align} P(H_1 \mid E) &= \frac{P(E \mid H_1)\,P(H_1)}{P(E \mid H_1)\,P(H_1)\;+\;P(E \mid H_2)\,P(H_2)} \\ \\ \ & = \frac{0.75 \times 0.5}{0.75 \times 0.5 + 0.5 \times 0.5} \\ \\ \ & = \frac{0.375}{0.375 + 0.25} \\ \\ \ & = \frac{0.375}{0.625} \\ \\ \ & = 0.6 \end{align}}

So, after seeing the plain cookie, the probability that Fred picked from Bowl #1 goes up from 0.5 to 0.6 (or 60%). This makes sense because Bowl #1 has more plain cookies!

How Bayesian Inference Works with More Data

Bayesian inference is great because you can keep updating your beliefs as you get more and more information. Each time you get new evidence, the "posterior probability" from the last step becomes the "prior probability" for the next step. This helps your beliefs get more and more accurate over time.

Predicting with Bayesian Inference

Bayesian inference can also be used to make predictions. Instead of just guessing one specific outcome, it gives you a whole range of possible outcomes and how likely each one is. This is often more helpful because it shows you the uncertainty involved.

For example, if you're trying to predict the weather, a Bayesian approach wouldn't just say "it will rain tomorrow." It might say, "there's a 70% chance of rain, a 20% chance of clouds, and a 10% chance of sun." This gives you a much clearer picture.

Where is Bayesian Inference Used?

Computer Applications

Bayesian inference is a big deal in computers and artificial intelligence.

• Spam Filters: Ever wonder how your email knows what's spam and what's not? Many spam filters use Bayesian inference! They learn from the words in emails you mark as spam versus those you don't. If an email has many words often found in spam (like "free money" or "urgent"), the filter uses Bayes' theorem to decide if it's likely to be spam.
• Pattern Recognition: Computers use it to recognize patterns, like faces in photos or objects in videos.
• Machine Learning: It's a key part of how many machine learning programs learn and make decisions.

Science and Healthcare

• Bioinformatics: This field uses computers to understand biological data, like genes. Bayesian inference helps scientists figure out which genes are active or how different biological processes work.
• Medical Research: In medicine, it can help estimate the risk of certain diseases or figure out how effective a new treatment might be, by combining what we already know with new study results.

In the Courtroom (Simplified)

Sometimes, people talk about using Bayesian inference in legal cases. Imagine a jury trying to decide if someone is responsible for something. They hear different pieces of evidence. Bayesian inference could be seen as a way to combine all that evidence step-by-step. The probability of a person's involvement would be updated as each new piece of evidence is presented.

However, using complex math like Bayes' theorem in a courtroom can be tricky because it might be hard for everyone to understand. The main idea is that it helps to logically combine all the information to reach a conclusion.

Other Uses

• Scientific Method: Some people think the scientific method itself is a form of Bayesian inference. Scientists start with a hypothesis, do experiments to get evidence, and then update their hypothesis based on the results.
• Searching for Lost Things: It's even used in search and rescue! If something is lost, like a plane or a ship, Bayesian search theory can help predict the most likely location based on all available information, guiding search teams.

History of Bayesian Inference

The ideas behind Bayesian inference go back to the 1700s.

• Thomas Bayes (1701–1761) was a British minister and mathematician who first showed how to use probabilities to understand unknown events.
• Pierre-Simon Laplace (1749–1827), a French mathematician, greatly expanded on Bayes' work. He used what is now called Bayes' theorem to solve many real-world problems, from understanding how planets move to medical statistics.

For a long time, this method was called "inverse probability." In the 20th century, other statistical methods became more popular. But in the 1980s, with the rise of powerful computers, Bayesian methods made a huge comeback. Computers made it possible to do the complex calculations needed for Bayesian inference, especially for complicated problems. Today, it's a widely used and important tool in many fields.

Images for kids

• 

  An example of how Bayesian inference can help archaeologists figure out the age of a site by updating their beliefs as new pottery fragments are found.

• 

  Adding up evidence, like pieces of a puzzle, to form a clearer picture.