Binary-coded decimal facts for kids

A binary clock might use LEDs to express binary values. In this clock, each column of LEDs shows a binary-coded decimal numeral of the traditional sexagesimal time.

In computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications (e.g. error or overflow).

In byte-oriented systems (i.e. most modern computers), the term unpacked BCD usually implies a full byte for each digit (often including a sign), whereas packed BCD typically encodes two digits within a single byte by taking advantage of the fact that four bits are enough to represent the range 0 to 9. The precise 4-bit encoding, however, may vary for technical reasons (e.g. Excess-3).

The ten states representing a BCD digit are sometimes called tetrades (the nibble typically needed to hold them is also known as a tetrade) while the unused, don't care-states are named pseudo-tetrad(e)s [de], pseudo-decimals or pseudo-decimal digits.

BCD's main virtue, in comparison to binary positional systems, is its more accurate representation and rounding of decimal quantities, as well as its ease of conversion into conventional human-readable representations. Its principal drawbacks are a slight increase in the complexity of the circuits needed to implement basic arithmetic as well as slightly less dense storage.

BCD was used in many early decimal computers, and is implemented in the instruction set of machines such as the IBM System/360 series and its descendants, Digital Equipment Corporation's VAX, the Burroughs B1700, and the Motorola 68000-series processors. BCD per se is not as widely used as in the past, and is unavailable or limited in newer instruction sets (e.g., ARM; x86 in long mode). However, decimal fixed-point and decimal floating-point formats are still important and continue to be used in financial, commercial, and industrial computing, where the subtle conversion and fractional rounding errors that are inherent in binary floating point formats cannot be tolerated.

Background

BCD takes advantage of the fact that any one decimal numeral can be represented by a four-bit pattern. The most obvious way of encoding digits is Natural BCD (NBCD), where each decimal digit is represented by its corresponding four-bit binary value, as shown in the following table. This is also called "8421" encoding.

This scheme can also be referred to as Simple Binary-Coded Decimal (SBCD) or BCD 8421, and is the most common encoding. Others include the so-called "4221" and "7421" encoding – named after the weighting used for the bits – and "Excess-3". For example, the BCD digit 6, 0110'b in 8421 notation, is 1100'b in 4221 (two encodings are possible), 0110'b in 7421, while in Excess-3 it is 1001'b ().

The following table represents decimal digits from 0 to 9 in various BCD encoding systems. In the headers, the "8 4 2 1" indicates the weight of each bit. In the fifth column ("BCD 8 4 −2 −1"), two of the weights are negative. Both ASCII and EBCDIC character codes for the digits, which are examples of zoned BCD, are also shown.

As most computers deal with data in 8-bit bytes, it is possible to use one of the following methods to encode a BCD number:

• Unpacked: Each decimal digit is encoded into one byte, with four bits representing the number and the remaining bits having no significance.
• Packed: Two decimal digits are encoded into a single byte, with one digit in the least significant nibble (bits 0 through 3) and the other numeral in the most significant nibble (bits 4 through 7).

As an example, encoding the decimal number 91 using unpacked BCD results in the following binary pattern of two bytes: Decimal: 9 1 Binary : 0000 1001 0000 0001

In packed BCD, the same number would fit into a single byte: Decimal: 9 1 Binary : 1001 0001

Hence the numerical range for one unpacked BCD byte is zero through nine inclusive, whereas the range for one packed BCD byte is zero through ninety-nine inclusive.

To represent numbers larger than the range of a single byte any number of contiguous bytes may be used. For example, to represent the decimal number 12345 in packed BCD, using big-endian format, a program would encode as follows: Decimal: 0 1 2 3 4 5 Binary : 0000 0001 0010 0011 0100 0101

Here, the most significant nibble of the most significant byte has been encoded as zero, so the number is stored as 012345 (but formatting routines might replace or remove leading zeros). Packed BCD is more efficient in storage usage than unpacked BCD; encoding the same number (with the leading zero) in unpacked format would consume twice the storage.

Shifting and masking operations are used to pack or unpack a packed BCD digit. Other bitwise operations are used to convert a numeral to its equivalent bit pattern or reverse the process.

Packed BCD

In packed BCD (or simply packed decimal), each nibble represent a decimal digit. Packed BCD has been in use since at least the 1960s and is implemented in all IBM mainframe hardware since then. Most implementations are big endian, i.e. with the more significant digit in the upper half of each byte, and with the leftmost byte (residing at the lowest memory address) containing the most significant digits of the packed decimal value. The lower nibble of the rightmost byte is usually used as the sign flag, although some unsigned representations lack a sign flag. As an example, a 4-byte value consists of 8 nibbles, wherein the upper 7 nibbles store the digits of a 7-digit decimal value, and the lowest nibble indicates the sign of the decimal integer value.

Standard sign values are 1100 (hex C) for positive (+) and 1101 (D) for negative (−). This convention comes from the zone field for EBCDIC characters and the signed overpunch representation. Other allowed signs are 1010 (A) and 1110 (E) for positive and 1011 (B) for negative. IBM System/360 processors will use the 1010 (A) and 1011 (B) signs if the A bit is set in the PSW, for the ASCII-8 standard that never passed. Most implementations also provide unsigned BCD values with a sign nibble of 1111 (F). ILE RPG uses 1111 (F) for positive and 1101 (D) for negative. These match the EBCDIC zone for digits without a sign overpunch. In packed BCD, the number 127 is represented by 0001 0010 0111 1100 (127C) and −127 is represented by 0001 0010 0111 1101 (127D). Burroughs systems used 1101 (D) for negative, and any other value is considered a positive sign value (the processors will normalize a positive sign to 1100 (C)).

No matter how many bytes wide a word is, there is always an even number of nibbles because each byte has two of them. Therefore, a word of n bytes can contain up to (2n)−1 decimal digits, which is always an odd number of digits. A decimal number with d digits requires 1/2(d+1) bytes of storage space.

For example, a 4-byte (32-bit) word can hold seven decimal digits plus a sign and can represent values ranging from ±9,999,999. Thus the number −1,234,567 is 7 digits wide and is encoded as: 0001 0010 0011 0100 0101 0110 0111 1101 1 2 3 4 5 6 7 −

Like character strings, the first byte of the packed decimal – that with the most significant two digits – is usually stored in the lowest address in memory, independent of the endianness of the machine.

In contrast, a 4-byte binary two's complement integer can represent values from −2,147,483,648 to +2,147,483,647.

While packed BCD does not make optimal use of storage (using about 20% more memory than binary notation to store the same numbers), conversion to ASCII, EBCDIC, or the various encodings of Unicode is made trivial, as no arithmetic operations are required. The extra storage requirements are usually offset by the need for the accuracy and compatibility with calculator or hand calculation that fixed-point decimal arithmetic provides. Denser packings of BCD exist which avoid the storage penalty and also need no arithmetic operations for common conversions.

Packed BCD is supported in the COBOL programming language as the "COMPUTATIONAL-3" (an IBM extension adopted by many other compiler vendors) or "PACKED-DECIMAL" (part of the 1985 COBOL standard) data type. It is supported in PL/I as "FIXED DECIMAL". Beside the IBM System/360 and later compatible mainframes, packed BCD is implemented in the native instruction set of the original VAX processors from Digital Equipment Corporation and some models of the SDS Sigma series mainframes, and is the native format for the Burroughs Corporation Medium Systems line of mainframes (descended from the 1950s Electrodata 200 series).

Ten's complement representations for negative numbers offer an alternative approach to encoding the sign of packed (and other) BCD numbers. In this case, positive numbers always have a most significant digit between 0 and 4 (inclusive), while negative numbers are represented by the 10's complement of the corresponding positive number. As a result, this system allows for 32-bit packed BCD numbers to range from −50,000,000 to +49,999,999, and −1 is represented as 99999999. (As with two's complement binary numbers, the range is not symmetric about zero.)

Fixed-point packed decimal

Fixed-point decimal numbers are supported by some programming languages (such as COBOL and PL/I). These languages allow the programmer to specify an implicit decimal point in front of one of the digits. For example, a packed decimal value encoded with the bytes 12 34 56 7C represents the fixed-point value +1,234.567 when the implied decimal point is located between the fourth and fifth digits: 12 34 56 7C 12 34.56 7+

The decimal point is not actually stored in memory, as the packed BCD storage format does not provide for it. Its location is simply known to the compiler, and the generated code acts accordingly for the various arithmetic operations.

Higher-density encodings

If a decimal digit requires four bits, then three decimal digits require 12 bits. However, since 2¹⁰ (1,024) is greater than 10³ (1,000), if three decimal digits are encoded together, only 10 bits are needed. Two such encodings are Chen–Ho encoding and densely packed decimal (DPD). The latter has the advantage that subsets of the encoding encode two digits in the optimal seven bits and one digit in four bits, as in regular BCD.

Zoned decimal

Some implementations, for example IBM mainframe systems, support zoned decimal numeric representations. Each decimal digit is stored in one byte, with the lower four bits encoding the digit in BCD form. The upper four bits, called the "zone" bits, are usually set to a fixed value so that the byte holds a character value corresponding to the digit. EBCDIC systems use a zone value of 1111 (hex F); this yields bytes in the range F0 to F9 (hex), which are the EBCDIC codes for the characters "0" through "9". Similarly, ASCII systems use a zone value of 0011 (hex 3), giving character codes 30 to 39 (hex).

For signed zoned decimal values, the rightmost (least significant) zone nibble holds the sign digit, which is the same set of values that are used for signed packed decimal numbers (see above). Thus a zoned decimal value encoded as the hex bytes F1 F2 D3 represents the signed decimal value −123: F1 F2 D3 1 2 −3

EBCDIC zoned decimal conversion table

(*) Note: These characters vary depending on the local character code page setting.

Fixed-point zoned decimal

Some languages (such as COBOL and PL/I) directly support fixed-point zoned decimal values, assigning an implicit decimal point at some location between the decimal digits of a number. For example, given a six-byte signed zoned decimal value with an implied decimal point to the right of the fourth digit, the hex bytes F1 F2 F7 F9 F5 C0 represent the value +1,279.50: F1 F2 F7 F9 F5 C0 1 2 7 9. 5 +0

BCD in computers

IBM

IBM used the terms Binary-Coded Decimal Interchange Code (BCDIC, sometimes just called BCD), for 6-bit alphanumeric codes that represented numbers, upper-case letters and special characters. Some variation of BCDIC alphamerics is used in most early IBM computers, including the IBM 1620 (introduced in 1959), IBM 1400 series, and non-Decimal Architecture members of the IBM 700/7000 series.

The IBM 1400 series are character-addressable machines, each location being six bits labeled B, A, 8, 4, 2 and 1, plus an odd parity check bit (C) and a word mark bit (M). For encoding digits 1 through 9, B and A are zero and the digit value represented by standard 4-bit BCD in bits 8 through 1. For most other characters bits B and A are derived simply from the "12", "11", and "0" "zone punches" in the punched card character code, and bits 8 through 1 from the 1 through 9 punches. A "12 zone" punch set both B and A, an "11 zone" set B, and a "0 zone" (a 0 punch combined with any others) set A. Thus the letter A, which is (12,1) in the punched card format, is encoded (B,A,1). The currency symbol $, (11,8,3) in the punched card, was encoded in memory as (B,8,2,1). This allows the circuitry to convert between the punched card format and the internal storage format to be very simple with only a few special cases. One important special case is digit 0, represented by a lone 0 punch in the card, and (8,2) in core memory.

The memory of the IBM 1620 is organized into 6-bit addressable digits, the usual 8, 4, 2, 1 plus F, used as a flag bit and C, an odd parity check bit. BCD alphamerics are encoded using digit pairs, with the "zone" in the even-addressed digit and the "digit" in the odd-addressed digit, the "zone" being related to the 12, 11, and 0 "zone punches" as in the 1400 series. Input/Output translation hardware converted between the internal digit pairs and the external standard 6-bit BCD codes.

In the Decimal Architecture IBM 7070, IBM 7072, and IBM 7074 alphamerics are encoded using digit pairs (using two-out-of-five code in the digits, not BCD) of the 10-digit word, with the "zone" in the left digit and the "digit" in the right digit. Input/Output translation hardware converted between the internal digit pairs and the external standard 6-bit BCD codes.

With the introduction of System/360, IBM expanded 6-bit BCD alphamerics to 8-bit EBCDIC, allowing the addition of many more characters (e.g., lowercase letters). A variable length Packed BCD numeric data type is also implemented, providing machine instructions that perform arithmetic directly on packed decimal data.

On the IBM 1130 and 1800, packed BCD is supported in software by IBM's Commercial Subroutine Package.

Today, BCD data is still heavily used in IBM processors and databases, such as IBM Db2, mainframes, and Power6. In these products, the BCD is usually zoned BCD (as in EBCDIC or ASCII), Packed BCD (two decimal digits per byte), or "pure" BCD encoding (one decimal digit stored as BCD in the low four bits of each byte). All of these are used within hardware registers and processing units, and in software. To convert packed decimals in EBCDIC table unloads to readable numbers, you can use the OUTREC FIELDS mask of the JCL utility DFSORT.

Other computers

The Digital Equipment Corporation VAX-11 series includes instructions that can perform arithmetic directly on packed BCD data and convert between packed BCD data and other integer representations. The VAX's packed BCD format is compatible with that on IBM System/360 and IBM's later compatible processors. The MicroVAX and later VAX implementations dropped this ability from the CPU but retained code compatibility with earlier machines by implementing the missing instructions in an operating system-supplied software library. This is invoked automatically via exception handling when the defunct instructions are encountered, so that programs using them can execute without modification on the newer machines.

The Intel x86 architecture supports a unique 18-digit (ten-byte) BCD format that can be loaded into and stored from the floating point registers, from where computations can be performed.

The Motorola 68000 series had BCD instructions.

In more recent computers such capabilities are almost always implemented in software rather than the CPU's instruction set, but BCD numeric data are still extremely common in commercial and financial applications. There are tricks for implementing packed BCD and zoned decimal add–or–subtract operations using short but difficult to understand sequences of word-parallel logic and binary arithmetic operations. For example, the following code (written in C) computes an unsigned 8-digit packed BCD addition using 32-bit binary operations:

uint32_t BCDadd(uint32_t a, uint32_t b)
{
    uint32_t t1, t2;    // unsigned 32-bit intermediate values

    t1 = a + 0x06666666;
    t2 = t1 ^ b;                   // sum without carry propagation
    t1 = t1 + b;                   // provisional sum
    t2 = t1 ^ t2;                  // all the binary carry bits
    t2 = ~t2 & 0x11111110;         // just the BCD carry bits
    t2 = (t2 >> 2) | (t2 >> 3);    // correction
    return t1 - t2;                // corrected BCD sum
}

BCD in electronics

BCD is very common in electronic systems where a numeric value is to be displayed, especially in systems consisting solely of digital logic, and not containing a microprocessor. By employing BCD, the manipulation of numerical data for display can be greatly simplified by treating each digit as a separate single sub-circuit. This matches much more closely the physical reality of display hardware—a designer might choose to use a series of separate identical seven-segment displays to build a metering circuit, for example. If the numeric quantity were stored and manipulated as pure binary, interfacing with such a display would require complex circuitry. Therefore, in cases where the calculations are relatively simple, working throughout with BCD can lead to an overall simpler system than converting to and from binary. Most pocket calculators do all their calculations in BCD.

The same argument applies when hardware of this type uses an embedded microcontroller or other small processor. Often, representing numbers internally in BCD format results in smaller code, since a conversion from or to binary representation can be expensive on such limited processors. For these applications, some small processors feature dedicated arithmetic modes, which assist when writing routines that manipulate BCD quantities.

Operations with BCD

Addition

It is possible to perform addition by first adding in binary, and then converting to BCD afterwards. Conversion of the simple sum of two digits can be done by adding 6 (that is, 16 − 10) when the five-bit result of adding a pair of digits has a value greater than 9. The reason for adding 6 is that there are 16 possible 4-bit BCD values (since 2⁴ = 16), but only 10 values are valid (0000 through 1001). For example: 1001 + 1000 = 10001 9 + 8 = 17

10001 is the binary, not decimal, representation of the desired result, but the most significant 1 (the "carry") cannot fit in a 4-bit binary number. In BCD as in decimal, there cannot exist a value greater than 9 (1001) per digit. To correct this, 6 (0110) is added to the total, and then the result is treated as two nibbles:

10001 + 0110 = 00010111 => 0001 0111 17 + 6 = 23 1 7

The two nibbles of the result, 0001 and 0111, correspond to the digits "1" and "7". This yields "17" in BCD, which is the correct result.

This technique can be extended to adding multiple digits by adding in groups from right to left, propagating the second digit as a carry, always comparing the 5-bit result of each digit-pair sum to 9. Some CPUs provide a half-carry flag to facilitate BCD arithmetic adjustments following binary addition and subtraction operations. The Intel 8080, the Zilog Z80 and the CPUs of the x86 family provide the opcode DAA (Decimal Adjust Accumulator).

Subtraction

Subtraction is done by adding the ten's complement of the subtrahend to the minuend. To represent the sign of a number in BCD, the number 0000 is used to represent a positive number, and 1001 is used to represent a negative number. The remaining 14 combinations are invalid signs. To illustrate signed BCD subtraction, consider the following problem: 357 − 432.

In signed BCD, 357 is 0000 0011 0101 0111. The ten's complement of 432 can be obtained by taking the nine's complement of 432, and then adding one. So, 999 − 432 = 567, and 567 + 1 = 568. By preceding 568 in BCD by the negative sign code, the number −432 can be represented. So, −432 in signed BCD is 1001 0101 0110 1000.

Now that both numbers are represented in signed BCD, they can be added together: 0000 0011 0101 0111 0 3 5 7 + 1001 0101 0110 1000 9 5 6 8 = 1001 1000 1011 1111 9 8 11 15

Since BCD is a form of decimal representation, several of the digit sums above are invalid. In the event that an invalid entry (any BCD digit greater than 1001) exists, 6 is added to generate a carry bit and cause the sum to become a valid entry. So, adding 6 to the invalid entries results in the following: 1001 1000 1011 1111 9 8 11 15 + 0000 0000 0110 0110 0 0 6 6 = 1001 1001 0010 0101 9 9 2 5

Thus the result of the subtraction is 1001 1001 0010 0101 (−925). To confirm the result, note that the first digit is 9, which means negative. This seems to be correct since 357 − 432 should result in a negative number. The remaining nibbles are BCD, so 1001 0010 0101 is 925. The ten's complement of 925 is 1000 − 925 = 75, so the calculated answer is −75.

If there are a different number of nibbles being added together (such as 1053 − 2), the number with the fewer digits must first be prefixed with zeros before taking the ten's complement or subtracting. So, with 1053 − 2, 2 would have to first be represented as 0002 in BCD, and the ten's complement of 0002 would have to be calculated.

Comparison with pure binary

Advantages

• Many non-integral values, such as decimal 0.2, have an infinite place-value representation in binary (.001100110011...) but have a finite place-value in binary-coded decimal (0.0010). Consequently, a system based on binary-coded decimal representations of decimal fractions avoids errors representing and calculating such values. This is useful in financial calculations.
• Scaling by a power of 10 is simple.
• Rounding at a decimal digit boundary is simpler. Addition and subtraction in decimal do not require rounding.
• The alignment of two decimal numbers (for example 1.3 + 27.08) is a simple, exact shift.
• Conversion to a character form or for display (e.g., to a text-based format such as XML, or to drive signals for a seven-segment display) is a simple per-digit mapping, and can be done in linear (O(n)) time. Conversion from pure binary involves relatively complex logic that spans digits, and for large numbers, no linear-time conversion algorithm is known (see Binary numeral system § Conversion to and from other numeral systems).

Disadvantages

• Some operations are more complex to implement. Adders require extra logic to cause them to wrap and generate a carry early. 15 to 20 per cent more circuitry is needed for BCD add compared to pure binary. Multiplication requires the use of algorithms that are somewhat more complex than shift-mask-add (a binary multiplication, requiring binary shifts and adds or the equivalent, per-digit or group of digits is required).
• Standard BCD requires four bits per digit, roughly 20 per cent more space than a binary encoding (the ratio of 4 bits to log₂10 bits is 1.204). When packed so that three digits are encoded in ten bits, the storage overhead is greatly reduced, at the expense of an encoding that is unaligned with the 8-bit byte boundaries common on existing hardware, resulting in slower implementations on these systems.
• Practical existing implementations of BCD are typically slower than operations on binary representations, especially on embedded systems, due to limited processor support for native BCD operations.

Representational variations

Various BCD implementations exist that employ other representations for numbers. Programmable calculators manufactured by Texas Instruments, Hewlett-Packard, and others typically employ a floating-point BCD format, typically with two or three digits for the (decimal) exponent. The extra bits of the sign digit may be used to indicate special numeric values, such as infinity, underflow/overflow, and error (a blinking display).

Signed variations

Signed decimal values may be represented in several ways. The COBOL programming language, for example, supports five zoned decimal formats, with each one encoding the numeric sign in a different way:

Telephony binary-coded decimal (TBCD)

3GPP developed TBCD, an expansion to BCD where the remaining (unused) bit combinations are used to add specific telephony characters, with digits similar to those found in telephone keypads original design.

The mentioned 3GPP document defines TBCD-STRING with swapped nibbles in each byte. Bits, octets and digits indexed from 1, bits from the right, digits and octets from the left.

bits 8765 of octet n encoding digit 2n

bits 4321 of octet n encoding digit 2(n – 1) + 1

Meaning number 1234, would become 21 43 in TBCD.

Alternative encodings

If errors in representation and computation are more important than the speed of conversion to and from display, a scaled binary representation may be used, which stores a decimal number as a binary-encoded integer and a binary-encoded signed decimal exponent. For example, 0.2 can be represented as 2×10⁻¹.

This representation allows rapid multiplication and division, but may require shifting by a power of 10 during addition and subtraction to align the decimal points. It is appropriate for applications with a fixed number of decimal places that do not then require this adjustment—particularly financial applications where 2 or 4 digits after the decimal point are usually enough. Indeed, this is almost a form of fixed point arithmetic since the position of the radix point is implied.

The Hertz and Chen–Ho encodings provide Boolean transformations for converting groups of three BCD-encoded digits to and from 10-bit values that can be efficiently encoded in hardware with only 2 or 3 gate delays. Densely packed decimal (DPD) is a similar scheme that is used for most of the significand, except the lead digit, for one of the two alternative decimal encodings specified in the IEEE 754-2008 floating-point standard.

Application

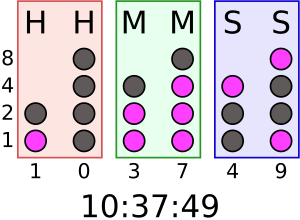
The BIOS in many personal computers stores the date and time in BCD because the MC6818 real-time clock chip used in the original IBM PC AT motherboard provided the time encoded in BCD. This form is easily converted into ASCII for display.

The Atari 8-bit family of computers used BCD to implement floating-point algorithms. The MOS 6502 processor has a BCD mode that affects the addition and subtraction instructions. The Psion Organiser 1 handheld computer's manufacturer-supplied software also entirely used BCD to implement floating point; later Psion models used binary exclusively.

Early models of the PlayStation 3 store the date and time in BCD. This led to a worldwide outage of the console on 1 March 2010. The last two digits of the year stored as BCD were misinterpreted as 16 causing an error in the unit's date, rendering most functions inoperable. This has been referred to as the Year 2010 problem.

Legal history

In the 1972 case Gottschalk v. Benson, the U.S. Supreme Court overturned a lower court's decision that had allowed a patent for converting BCD-encoded numbers to binary on a computer. The decision noted that a patent "would wholly pre-empt the mathematical formula and in practical effect would be a patent on the algorithm itself". This was a landmark judgement that determining the patentability of software and algorithms.

See also

In Spanish: Decimal codificado en binario para niños

• Bi-quinary coded decimal
• Binary-coded ternary (BCT)
• Binary integer decimal (BID)
• Bitmask
• Chen–Ho encoding
• Decimal computer
• Densely packed decimal (DPD)
• Double dabble, an algorithm for converting binary numbers to BCD
• Year 2000 problem