Combination (mathematics) facts for kids
In math, a combination is a way to choose items from a larger group where the order you pick them in doesn't matter. Think of it like picking ingredients for a pizza – it doesn't matter if you add the pepperoni before the mushrooms or after, you still end up with the same pizza! The study of counting these possibilities is called Combinatorics.
When the order does matter, it's called a permutation. For example, if you're picking a password, "123" is different from "321". Because order matters for permutations, there are always more permutations than combinations for the same set of items. If you pick the numbers 1, 3, and 5, there's only one combination of {1,3,5}. But there are six permutations: {1,3,5}, {1,5,3}, {3,1,5}, {3,5,1}, {5,1,3}, and {5,3,1}.
Contents
What is a Combination?
A combination is simply a selection of items from a larger set. The key idea is that the order of the items you pick doesn't change the combination itself. For example, if you have three friends, Alex, Ben, and Chloe, and you want to pick two of them to go to the movies, picking Alex then Ben is the same as picking Ben then Alex. Both choices result in the same group of two friends.
Combinations vs. Permutations
It's easy to get combinations and permutations mixed up! Here's a simple way to remember the difference:
- Combinations: Order doesn't matter. Think of a "combination" lock – wait, that's actually a permutation lock because the order you dial the numbers does matter! A better example is picking a hand of cards in a game. The order you get the cards doesn't change your hand.
- Permutations: Order matters. Think of arranging books on a shelf. Putting "Book A" first and "Book B" second is different from putting "Book B" first and "Book A" second.
Real-World Examples
- Combination: Choosing 3 flavors of ice cream from 10 available flavors. The order you choose them doesn't change the scoop.
- Permutation: Arranging 3 different books on a shelf. The order creates a different arrangement.
- Combination: Selecting 5 players for a basketball team from a group of 12. The team is the same regardless of who you pick first.
- Permutation: Deciding the finishing order of runners in a race. First, second, and third place are distinct positions.
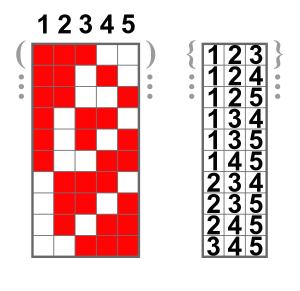
How to Calculate Combinations
There's a special formula to figure out how many combinations are possible. If you want to choose k items from a total of n items, the number of combinations is written as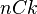 
or 
.
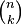The formula looks like this: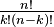 
Let's break down what the "!" means. In math, "!" stands for factorial. A factorial means you multiply a number by every whole number smaller than it, all the way down to 1.
- For example, 5! (read as "five factorial") is 5 × 4 × 3 × 2 × 1 = 120.
- And 3! is 3 × 2 × 1 = 6.
- By definition, 0! is equal to 1.
Using the Formula: An Example
Let's say you have 5 different fruits (apples, bananas, cherries, dates, and elderberries) and you want to pick 3 of them to make a fruit salad. How many different combinations of 3 fruits can you make?
Here, n (total number of items) is 5, and k (number of items you want to choose) is 3.
1. First, find n!: 5! = 5 × 4 × 3 × 2 × 1 = 120
2. Next, find k!: 3! = 3 × 2 × 1 = 6
3. Then, find (n - k)!: (5 - 3)! = 2! = 2 × 1 = 2
4. Now, put these numbers into the formula: 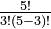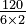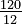Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tfrac{5!}{3!(5-3)!} = Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tfrac{120}{6 \times 2} = Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tfrac{120}{12} = 10
So, there are 10 different combinations of 3 fruits you can pick from a group of 5.
This number is also known as a binomial coefficient, which you might learn more about in higher-level math.
Related pages
- Pascal's Triangle
- Superpermutation
