Continuum (mathematics) facts for kids
In mathematics, especially in a field called set theory, the continuum is a special idea. It can mean two things:
- All the real numbers themselves.
- Or, the "size" of the set of real numbers. This "size" is called cardinality.
Imagine a number line that stretches on forever in both directions. Every single point on that line represents a real number. The continuum is about how many of these points there are. It's a huge, endless amount!
The continuum hypothesis is a famous guess in mathematics. It suggests that the "size" of the real numbers is the same as something called aleph one. Aleph one is the "next biggest" type of infinity after the infinity of counting numbers (like 1, 2, 3...).
What's really interesting is that mathematicians have found that this guess (the continuum hypothesis) can't be proven true or false using the basic rules of set theory. It's like a puzzle piece that fits perfectly whether it's there or not!
Contents
What are Real Numbers?
Real numbers are all the numbers you can think of that can be placed on a number line. This includes:
- Counting numbers: Like 1, 2, 3, and so on.
- Whole numbers: These are counting numbers plus zero (0, 1, 2, 3...).
- Integers: These are whole numbers and their negative partners (...-2, -1, 0, 1, 2...).
- Fractions: Numbers like 1/2, 3/4, or -7/5.
- Decimals: Numbers like 0.5, 3.14, or -2.75. Some decimals stop, and some go on forever in a repeating pattern (like 1/3 = 0.333...).
- Irrational numbers: These are special decimals that go on forever without any repeating pattern. Famous examples are pi (about 3.14159...) and the square root of 2 (about 1.41421...).
So, real numbers cover everything on the number line, with no gaps!
What is a Set?
In mathematics, a set is simply a collection of things. These "things" are called elements or members of the set. For example:
- A set of fruits could be {apple, banana, orange}.
- A set of numbers could be {1, 2, 3, 4, 5}.
- The set of all real numbers is a very large set.
Sets help mathematicians organize and study different groups of items, especially when dealing with very large or infinite collections.
What is Cardinality?
Cardinality is a fancy word for the "size" of a set. It tells you how many elements are in a set.
- For a small set like {apple, banana, orange}, the cardinality is 3.
- For the set of counting numbers {1, 2, 3, ...}, the cardinality is infinite. This type of infinity is called aleph null (written as
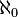). It's the "smallest" kind of infinity.
Mathematicians discovered that not all infinities are the same size! Some infinite sets are "bigger" than others. The cardinality of the real numbers is a "bigger" infinity than aleph null. This "bigger" infinity is what we call the continuum.
The Continuum Hypothesis
The continuum hypothesis asks a big question: Is the "size" of the real numbers (the continuum) the very next size of infinity after aleph null?
- We know the counting numbers have a size of aleph null ().
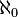- The next "biggest" size of infinity is called aleph one (
).
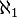The hypothesis suggests that the cardinality of the continuum is exactly aleph one. In simpler terms, it asks if there are any "sizes of infinity" in between the size of the counting numbers and the size of the real numbers.
For a long time, mathematicians tried to prove or disprove this hypothesis. But in the 1960s, Paul Cohen showed something amazing:
- You can't prove the continuum hypothesis is true using the standard rules of set theory.
- You also can't prove it's false using those same rules.
This means the continuum hypothesis is independent of the basic rules of set theory. It's like an extra rule you could choose to add or not add to the system, and the system would still work perfectly fine either way! This was a huge discovery in mathematics.
Related pages
