Date of Easter facts for kids
Easter is a special holiday that doesn't fall on the same date every year. It's called a moveable feast because its date changes. To figure out when Easter will be, people use a special calculation called Computus Paschalis (which means "Easter computation").
Easter is always celebrated on the first Sunday after the Paschal full moon. This "Paschal full moon" is a way to estimate the first full moon that happens on or after March 21st. March 21st is chosen because it's close to the March equinox, which is when day and night are about equal length.
The way Easter's date is calculated is a bit tricky. It needs to connect the lunar months (based on the Moon's cycles) with the solar year (based on the Sun's cycle). It also considers the day of the week and the date in either the Julian calendar or the Gregorian calendar. The calculation is complex because early Christians wanted Easter to be linked to the Jewish holiday of Passover, which is when they believe Jesus was crucified.
Long ago, the pope would announce the date of Easter each year. But as communication became harder in the Roman Empire, the church wanted a way for local leaders to figure out the date themselves. They also wanted to set the date without relying on the Hebrew calendar, using the March equinox instead.
The calculations for Easter give different results depending on which calendar is used. The Catholic Church and Protestant churches use the Gregorian calendar, while most Eastern and Oriental Orthodoxy churches use the Julian calendar. This is why they celebrate Easter on different days. The Gregorian calendar was created to fix a problem: March 21st was no longer lining up with the actual equinox.
Contents
History of Easter Calculation
The first known ways to calculate Easter in Rome were created around 222 AD. These used an eight-year cycle. Later, 84-year tables were used. Around 277 AD, Bishop Anatolius of Laodicea suggested a method based on a 19-year cycle, which became very important later.
The method from Alexandria (a city in Egypt) became the main way to calculate Easter in the late 300s. This method was later changed to fit the Julian calendar around 440 AD. This led to an Easter table that covered years from 437 to 531. A monk named Dionysius Exiguus in Rome then continued this table, covering years 532 to 616. Dionysius also introduced the Christian Era, which counts years from the birth of Christ, when he published his new Easter table in 525 AD.
In the 4th century, Rome adopted a different 84-year cycle. Later, in 457 AD, Victorius of Aquitaine tried to combine the Alexandrian method with Roman rules, creating a 532-year table. However, his tables had some big mistakes. These Victorian tables were used in places like France and Spain until the Dionysian tables replaced them in the late 700s.
The tables used by Dionysius and Victorius didn't match the ones used in the British Isles. The British tables also used an 84-year cycle, but they had an error that made the full moons appear too early. This caused confusion, like when Queen Eanflæd was fasting for Palm Sunday while her husband, King Oswiu, was feasting for Easter Sunday because they followed different calculations!
Because of this confusion, the southern Irish started using the Dionysian tables after a meeting in 630 AD. The northern English followed after another meeting in 664 AD.
The Dionysian way of calculating Easter was fully explained by Bede in 725 AD. It was likely adopted by Charlemagne for the Frankish Church around 782 AD. This method stayed in use in Western Europe until the Gregorian calendar reform. Most Eastern Churches, including the Eastern Orthodox Church, still use it today. Only the Finnish Orthodox Church uses the Gregorian system.
Over time, the calculated date for the spring equinox (March 21st) in the Julian calendar started to drift from the actual astronomical equinox. Also, the way the Moon's phases were calculated in the 19-year cycle became inaccurate, being off by about one day every 310 years. By the 1500s, the lunar calendar was about four days out of sync with the real Moon. These problems led to the Gregorian reform of the calendar in 1582. The Roman Catholic Church started using the Gregorian Easter in 1583, and most Protestant churches adopted it between 1753 and 1845.
Some German Protestant states and Sweden used an "astronomical Easter" for a while (1700-1776 for Germany, 1739-1844 for Sweden). This was based on actual observations of the Sun and Moon.
At the Second Vatican Council, the Catholic Church said it would be okay to move Easter to a fixed Sunday if all Christian churches could agree on a date.
How Easter is Calculated
The Easter calculation groups days into "lunar months," which are either 29 or 30 days long. A lunar year has 12 lunar months, making it about 354 or 355 days long. This is about 11 days shorter than a regular calendar year (365 or 366 days). These extra 11 days are called epacts. They help us figure out the correct day in the lunar year.
When the epact reaches 30 or more, an extra "intercalary month" (a 30-day month) is added to the lunar calendar. Then, 30 is subtracted from the epact.
The 19-year Metonic cycle is important here. It assumes that 19 solar years are about the same length as 235 lunar months. This means that after 19 years, the Moon's phases should repeat in the same way in the solar year. The "golden number" tells you where a year is in this 19-year cycle. You can find it by dividing the year by 19 and adding 1 to the remainder.
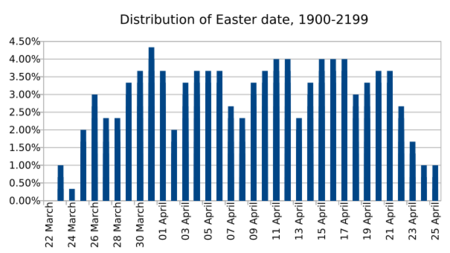
The "Paschal month" is the first lunar month of the year where its 14th day (which is considered the full moon) falls on or after March 21st. Easter is then the Sunday after this 14th day. This means Easter always falls between March 22nd and April 25th.
Gregorian Calendar Changes
When the Gregorian calendar was introduced in 1582, a new way to calculate Easter was also created. This method was explained by Clavius.
Easter is the Sunday after the Paschal full moon. The Paschal full moon is the church's calculated full moon on or after March 21st. The 14th day of the lunar month is considered the day of the full moon.
The Gregorian method finds new moon dates by figuring out the epact for each year. The epact is like the age of the moon on January 1st.
The date of the Paschal full moon in a specific year is usually 11 days earlier than the previous year, or 19 days later. This pattern helps keep the lunar calendar in sync.
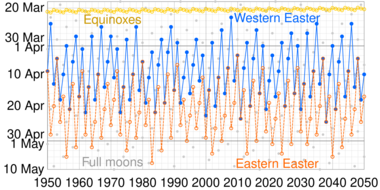
In the Eastern system, the Paschal full moon is usually four days later than in the West. This is because of the different calendar systems.
How the Calendar Table Works
To calculate Easter, a table called the calendarium is used. Imagine a table of all 365 days of the year. Each date is given a special label, counting downwards from "*" (0 or 30) to "i" (1), starting from January 1st. This pattern repeats.
The "epact" for a year tells you which dates are "new moons" for that year. For example, if the epact is 27, then any date with the label "xxvii" (27) is an ecclesiastical new moon. The ecclesiastical full moon happens 13 days later.
Then, you need to find the "dominical letter" for the year. This letter tells you which day of the week is Sunday. For example, if January 5th is a Sunday and has the letter "E", then every date with the letter "E" is a Sunday that year.
Once you have the epact and the dominical letter, you can find the Paschal full moon. This is the first ecclesiastical full moon on or after March 21st. Easter Day is the first Sunday after this Paschal full moon.
For example, if the epact is 27, new moons fall on March 4th and April 3rd. This means full moons are on March 17th and April 16th. The Paschal full moon (on or after March 21st) would be April 16th. If the dominical letter is "E", and April 16th is a Thursday, then the next Sunday (Easter) would be April 20th.


| Epact label |
March | DL | April | DL |
|---|---|---|---|---|
| * | 1 | D | ||
| xxix | 2 | E | 1 | G |
| xxviii | 3 | F | 2 | A |
| xxvii | 4 | G | 3 | B |
| xxvi | 5 | A | 4 | C |
| 25 | 6 | B | ||
| xxv | 5 | D | ||
| xxiv | 7 | C | ||
| xxiii | 8 | D | 6 | E |
| xxii | 9 | E | 7 | F |
| xxi | 10 | F | 8 | G |
| xx | 11 | G | 9 | A |
| xix | 12 | A | 10 | B |
| xviii | 13 | B | 11 | C |
| xvii | 14 | C | 12 | D |
| xvi | 15 | D | 13 | E |
| xv | 16 | E | 14 | F |
| xiv | 17 | F | 15 | G |
| xiii | 18 | G | 16 | A |
| xii | 19 | A | 17 | B |
| xi | 20 | B | 18 | C |
| x | 21 | C | 19 | D |
| ix | 22 | D | 20 | E |
| viii | 23 | E | 21 | F |
| vii | 24 | F | 22 | G |
| vi | 25 | G | 23 | A |
| v | 26 | A | 24 | B |
| iv | 27 | B | 25 | C |
| iii | 28 | C | 26 | D |
| ii | 29 | D | 27 | E |
| i | 30 | E | 28 | F |
| * | 31 | F | 29 | G |
| xxix | 30 | A |
Corrections and Adjustments
The Gregorian calendar includes corrections to keep the Easter date accurate over long periods. These are called "solar corrections" and "lunar corrections." Solar corrections adjust for leap days that are skipped in certain century years. Lunar corrections adjust for small errors that build up in the Moon's cycle over centuries. These corrections ensure that the calculated Easter date stays close to the actual astronomical events.
The system is designed so that Easter never falls later than April 25th. This means that sometimes, if the calculation would put Easter on April 26th, it is moved back to April 19th. This makes April 19th a very common Easter date.
The dates of Easter repeat in the same order only after a very long time—about 5.7 million years! This is because of the complex way the solar and lunar corrections interact. However, the calendar would need to be adjusted much sooner than that because the Earth's rotation and the Moon's orbit are slowly changing.
British Calendar Act
In Britain, before 1752, Easter was calculated using a simple table in the Book of Common Prayer. When Britain adopted the Gregorian calendar in 1752, a new law called the Calendar (New Style) Act 1750 changed how Easter was calculated to match the Gregorian rules. This law made sure that the dates in the Book of Common Prayer were updated. The law stated that Easter Day is always the first Sunday after the Full Moon that happens on or after March 21st. If the Full Moon falls on a Sunday, Easter is the Sunday after that.
"Paradoxical" Easter Dates
Sometimes, the calculated date for Easter can be different from what it would be if it were based on exact astronomical observations. These differences are called "paradoxical" Easter dates. This happens because the calculations use approximations of the Moon's phases and the spring equinox.
For example, if the astronomical full moon happens on a Sunday, but the calculation says Easter should be that same Sunday, it's celebrated a week earlier than the "astronomically correct" date. Or, if the astronomical full moon is on a Saturday, and Easter is celebrated a week later than that Sunday, it's a week too late.
These differences can also be larger, sometimes four or five weeks, if the calculated equinox or full moon is very different from the real one. These "paradoxes" show how complex it is to create a calendar system that perfectly matches both the Sun and Moon's movements over long periods.
See also
 In Spanish: Computus para niños
In Spanish: Computus para niños
- Christian Zeller
- Crucifixion darkness
- Reform of the date of Easter
External links
- Excel spreadsheet formulae and functions to calculate Easter
- The Complete Works of Venerable Bede Vol. 6 (Contains De Temporibus and De Temporum Ratione.)
- The entry on epacts in the Catholic Encyclopedia of 1911
- The original texts of the Gregorian calendar reform (in Latin), with translations into French by Rodolphe Audette
- An Easter calculator with an extensive bibliography, and with useful links
- Ephemeris site of the Bureau des Longitudes with an Easter calculator (valid between 325 and 2500)
- A calendar page and calculator by Holger Oertel
- A page from Clive Feather with a brief explanation, some more tables, and another algorithm
- An extensive calendar site and calendar and Easter calculator by Nikolaus A. Bär
- Explanation of the Gregorian solar and lunar calendar, with improved procedures over the tabular method, by David Madore
- Dionysius Exiguus' Easter table
- Mnemonic Computus Diagrams of Hands from manuscript in The British Library
- St. Gallen, Stiftsbibliothek, Codex Sangallensis 378 (11th century) p. 28. Contains the poem Nonae Aprilis norunt quinos.
- A simplified method for determining the date of Easter for all years 326 to 4099 by Ronald W. Mallen
- Text of the Calendar (New Style) Act 1750, British Act of Parliament introducing the Gregorian Calendar as amended to date. Contains tables for calculating Easter up until the year 8599. Contrast with the Act as passed.
- Computuslat A database of medieval manuscripts containing Latin computistical algorithms, texts, tables, diagrams and calendars.