Ellipse facts for kids

An ellipse is a cool shape that looks like an oval or a flattened circle. Think of it like a squished circle!

In geometry, an ellipse is a special kind of curve you can find on a flat surface. It's made when you slice through a cone with a flat plane in a certain way. This cut creates a closed, oval-shaped curve.

An ellipse obtained as the intersection of a cone with a plane.

Did you know that circles are actually a special type of ellipse? You get a circle when the cutting plane slices the cone perfectly straight across, at a right angle to its center.

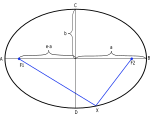
An ellipse also has a special property: if you pick any point on its curve, the total distance from that point to two fixed points inside the ellipse is always the same. These two fixed points are called the foci (pronounced FOH-sigh). A circle has just one center, but an ellipse has two foci!

An ellipse and its properties.

You can easily draw an ellipse using this idea! Imagine putting two pins into a piece of cardboard. Then, take a loop of string and put it around both pins. Now, use a pencil to pull the string tight and move the pencil around. The path your pencil draws will be an ellipse!

This is how planets orbit the sun! The path they take around the sun is an ellipse, with the sun at one of the foci. There's nothing special at the other focus, just an empty spot.

Drawing Ellipses Easily

Ellipses are often seen in drawings and designs as the way circles look when viewed from an angle. Because of this, it's really helpful to know how to draw them. Today, the best way to draw an ellipse is with a computer.

Before computers, people used special tools called ellipsographs to draw ellipses smoothly, just like you use a compass to draw a circle. Even ancient Greek mathematicians like Archimedes knew about the ideas behind these tools!

If you don't have an ellipsograph, there are still some clever ways to draw an ellipse. For most of these methods, you need to know the size and shape of the ellipse you want to draw.

The Pins-and-String Method

Ellipse: gardener's method

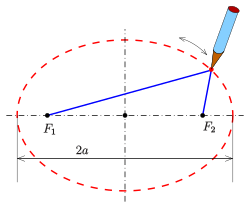
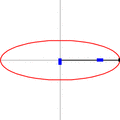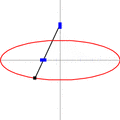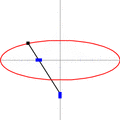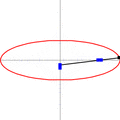
This method uses the special property of an ellipse: that the sum of the distances from any point on the curve to its two foci is always the same.

Here's how to do it:

• Push two drawing pins into a piece of paper. These pins will be the two foci of your ellipse.
• Tie a piece of string into a loop.
• Put the string loop around the two pins.
• Place the tip of a pencil inside the loop and pull the string tight to form a triangle.
• Now, move the pencil around while keeping the string tight. The pencil will trace out a perfect ellipse!

This method is so simple and useful that gardeners even use it with two pegs and a rope to outline elliptical flower beds. That's why it's sometimes called the gardener's ellipse!

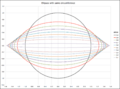
The Paper Strip Method

Ellipse construction: paper strip method 1

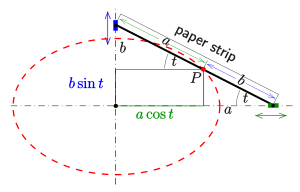
This is another cool way to draw an ellipse, and it uses a simple strip of paper. You need to know the length of the ellipse's long side (called 'a') and its short side (called 'b').

Here's how it works:

• Take a strip of paper.
• Mark a point on the strip. This point should be 'b' distance from one end and 'a' distance from the other end. So the total length of the strip from the 'a' end to the 'b' end is 'a+b'.
• Now, slide the ends of the paper strip along two straight lines that cross each other at a right angle (like the X and Y axes on a graph).
• As you slide the strip, the marked point on the paper will trace out an ellipse!

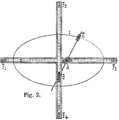
This method can even be done with a special mechanical device called a Tusi couple. It's also similar to what happens if you stand in the middle of a ladder that's sliding down a slippery wall while its base slides on a slippery floor – your feet would trace an ellipse!

Images for kids

• 

  Ellipse: Steiner generation

• 

  An ellipse (in red) as a special case of the hypotrochoid with R = 2r

• 

  The area enclosed by a tilted ellipse is \pi\; y_\text{int}\, x_\text{max}.

• 

  Ellipses with same circumference

• 

  Wave pattern of a little droplet dropped into mercury in one focus of the ellipse

• 

  Animation of the method

• 

  Ellipses with Tusi couple. Two examples: red and cyan.

• 

  Animation of the variation of the paper strip method 1

• 

  Trammel of Archimedes (principle)

• 

  Ellipsograph due to Benjamin Bramer

• 

  Variation of the paper strip method 2

• 

  Ellipsoid

• 

  Elliptic cone

• 

  Elliptic cylinder

• 

  Hyperboloid of one sheet

• 

  Hyperboloid of two sheets

See also

In Spanish: Elipse para niños