Ergodic theory facts for kids

Ergodic theory (from Greek words meaning "work" and "way") is a part of mathematics. It looks at how systems behave over a long time. Imagine a system, like a stirred pot of soup. Ergodic theory helps us understand if, after a long time, the soup is perfectly mixed.

It studies dynamical systems. These are systems where things change over time following clear rules, without any random parts. Ergodic theory helps us predict the "average" behavior of these systems.

This field uses ideas from measure theory, which is about measuring sizes of sets. It first started to help solve problems in statistical physics, which studies how large groups of particles behave.

A main goal of ergodic theory is to see what happens to a system after it runs for a very long time. The Poincaré recurrence theorem is an early idea here. It says that almost all parts of a system will eventually return close to their starting point. Systems that follow this rule are called conservative systems. All ergodic systems are conservative.

What are Ergodic Systems?

Ergodic theory often talks about ergodic transformations. Think of a transformation as an action that changes something. If you have a set of things, an ergodic transformation mixes them up very well.

Imagine you have a bowl of hot oatmeal. You drop a spoonful of syrup into it. If you keep stirring the oatmeal (this is like applying an ergodic transformation), the syrup will not stay in one spot. Instead, it will spread out evenly through all the oatmeal. At the same time, the stirring doesn't squeeze or stretch any part of the oatmeal. It just moves it around. This means it keeps the "measure" or density the same.

In math, a transformation T is ergodic if it mixes things so well that any part of the system that stays the same after the transformation must either be almost empty or almost the whole system.

Examples of Ergodic Behavior

Evolution of a group of classical systems in a "phase space" (top). The systems are particles in a potential well (red curve, bottom). A group of particles that starts close together gets swirled around over time. This shows how systems can spread out in their possible states.

• Imagine a point moving around a circle. If it moves by an amount that is an irrational number (like Pi), it will eventually visit every part of the circle. This is an ergodic movement.
• Think of a Bernoulli shift. This is like flipping a coin many times. The sequence of coin flips is ergodic. This means that if you look at a very long sequence of flips, the number of heads and tails will be about what you expect.
• In a continuous dynamical system, ergodicity means that the path of the system "spreads out" everywhere in its possible space. If a system has a compact space and something that always stays the same (a "first integral"), it cannot be ergodic. This is like a ball rolling in a bowl; it stays within the bowl and doesn't go everywhere.

Ergodic Theorems: Time vs. Space Averages

A big part of ergodic theory is about "ergodic theorems." These theorems say that under certain conditions, the average behavior of a system over a long time is the same as its average behavior across all possible states.

Let's look at two types of averages:

• Time average: This is what you get if you watch one part of the system for a very long time and average its properties. For example, if you watch one particle in a gas and average its speed over many hours.
• Space average: This is what you get if you take a snapshot of the entire system at one moment and average the properties of all its parts. For example, if you measure the speed of every particle in the gas at a single moment and average them.

Normally, these two averages might be different. But if a system is ergodic, and its "measure" (like the total amount of gas) stays the same, then the time average and the space average will be the same for almost all starting points.

This important idea comes from the pointwise ergodic theorem by George David Birkhoff. It says that if you watch a system for a very long time, the average of what you see will settle down to a specific value. If the system is ergodic, this value will be the same as the average you would get by looking at all possible states of the system at once.

For example, if you have a gas, the average speed of one particle over a very long time will be the same as the average speed of all particles in the gas at any given moment.

Sojourn Time

The sojourn time is the amount of time a system spends in a certain measurable area. For example, how long a particle stays in a specific part of a container.

A cool result of the ergodic theorem is that in an ergodic system, the proportion of time a system spends in a certain area is equal to the "size" of that area compared to the whole system.

So, if you have a small area A, the system will spend less time in A than in a larger area. The average time it takes for the system to return to area A is related to how small A is. The smaller the area, the longer it takes to come back to it.

Images for kids

• 

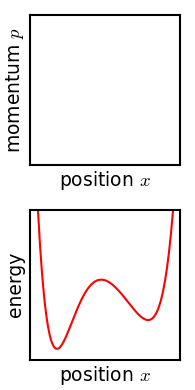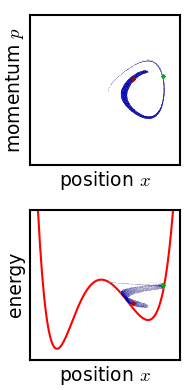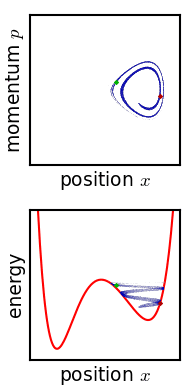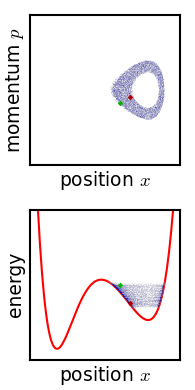
  Evolution of an ensemble of classical systems in phase space (top). The systems are massive particles in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time and "spread around" phase space. This is however not ergodic behaviour since the systems do not visit the left-hand potential well.

See also

In Spanish: Teoría ergódica para niños