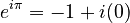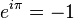Euler's identity Facts for Kids

A visual representation of Euler's identity.

Euler's identity, also known as Euler's equation, is a very famous and beautiful equation in mathematics. It looks like this:

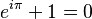
$e^{i\pi} + 1 = 0$

This equation brings together five of the most important numbers in mathematics:

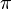$\pi$ (pi): This number is about circles. It's the ratio of a circle's distance around (circumference) to its distance across (diameter). Pi is approximately 3.14159.
$e$ (Euler's Number): This special number is important in areas like growth and decay, and it's used in many science and engineering calculations. It's approximately 2.71828.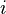
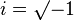$i$ (imaginary unit): This is a special number that helps us work with square roots of negative numbers. By definition, $i = \surd{-1}$ .

The identity also uses three basic math actions: adding, multiplying, and raising to a power (exponentiation).

Euler's identity is named after Leonard Euler, a brilliant mathematician from Switzerland. It's not fully clear if he was the first to discover it.

Many mathematicians and scientists think this identity is incredibly important. In a poll by Physics World magazine, people called it "the most profound mathematical statement ever written" and "filled with cosmic beauty."

How to Understand Euler's Identity
Related pages
Images for kids
See also

How to Understand Euler's Identity

You can show that Euler's identity is true using something called a Taylor series. Imagine breaking down a complicated math function into a long list of simpler additions. This is what a Taylor series does.

For example, the exponential function 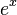$e ^{x}$ can be written as an endless sum:

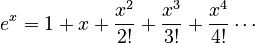
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e ^{x} = 1 + x + {x^{2}\over{2!}} + {x^{3}\over{3!}} + {x^{4}\over{4!}} \cdots

The sine function 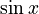Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin{x} can also be written as a series:

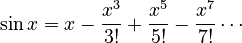
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin{x} = x - {x^{3} \over 3!} + {x^5 \over 5!} - {x^{7} \over 7!} \cdots

And the cosine function 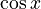Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos{x} can be written as:

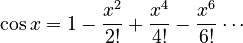
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos{x} = 1 - {x^{2} \over 2!} + {x^4 \over 4!} - {x^{6} \over 6!} \cdots

Now, let's look at a related formula called Euler's formula: 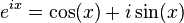$e^{ix} = \cos(x) + i \sin(x)$ . This formula connects the exponential function with sine and cosine.

If we put ix into the series for 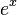$e^x$ , we get:

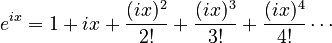
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{ix} = 1 + ix + {(ix)^{2}\over{2!}} + {(ix)^{3}\over{3!}} + {(ix)^{4}\over{4!}} \cdots

Since 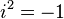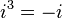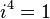$i^2 = -1$ , $i^3 = -i$ , $i^4 = 1$ , and so on, this series becomes:

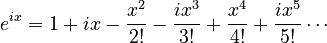
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{ix} = 1 + ix - {x^{2} \over 2!} - {ix^{3} \over 3!} + {x^{4} \over 4!} + {ix^{5} \over 5!} \cdots

Now, let's look at the series for 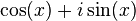$\cos(x) + i \sin(x)$ :

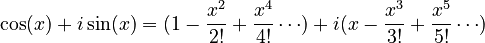
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos(x) + i \sin(x) = ( 1 - {x^{2} \over 2!} + {x^{4} \over 4!} \cdots) + i(x - {x^{3} \over 3!} + {x^{5} \over 5!}\cdots)

If we combine these terms, we get:

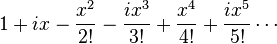
$1 + ix - {x^{2} \over 2!} - {ix^{3} \over 3!} + {x^{4} \over 4!} + {ix^{5} \over 5!} \cdots$

You can see that the series for 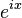$e^{ix}$ is exactly the same as the series for 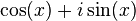$\cos(x) + i \sin(x)$ ! This proves that:

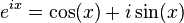
$e^{ix} = \cos(x) + i \sin(x)$

To get Euler's identity, we just replace x with 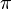$\pi$ (pi) in this formula:

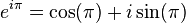
$e^{i\pi} = \cos(\pi) + i \sin(\pi)$

We know that 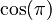Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos(\pi) (cosine of 180 degrees) is -1, and 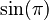Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin(\pi) (sine of 180 degrees) is 0. So, the equation becomes:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{i\pi} = -1 + i(0)
$e^{i\pi} = -1$

Finally, if we add 1 to both sides, we get Euler's identity:

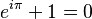
$e^{i\pi} + 1 = 0$

Images for kids

This animation shows how the value of Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (1 + {{sfrac|''iπ''|''N''}})''N'' gets closer and closer to -1 as N gets larger.

Euler's identity facts for kids

Contents

How to Understand Euler's Identity

Related pages

Images for kids

See also