−1 (number) facts for kids
Quick facts for kids −1 |
|||
|---|---|---|---|
|
List of numbers -- Integers (whole numbers) |
|||
| Cardinal | −1, minus one, negative one | ||
| Arabic | −١ | ||
| Chinese numeral | 负一,负弌,负壹 | ||
| Bengali | ô১ | ||
| Binary (byte) |
|
||
| Hex (byte) |
|
||
In mathematics, −1 is a special integer. It is the number you add to 1 to get 0. Think of it as the "opposite" of 1. If you have 1 apple and someone takes 1 apple away, you have 0 apples left.
Negative one is a negative number. It sits on the number line between negative two (−2) and zero (0). It has some things in common with positive one, but also some big differences!
In computer science, −1 is often used as a starting number for counting. It can also show that a computer program hasn't found any useful information yet. It's like a placeholder.
Contents
What Happens When You Multiply by -1?
Multiplying any number by −1 simply changes its sign. For example, if you multiply 5 by −1, you get −5. If you multiply −5 by −1, you get 5.
This happens because −1 is the "additive inverse" of 1. This means that when you add 1 and −1 together, you get 0.
Squaring -1: What's the Result?
When you square a number, you multiply it by itself. So, squaring −1 means you multiply −1 by −1. The amazing thing is that −1 multiplied by −1 equals 1!
This is why the square of any negative number is always a positive number. For example, −2 times −2 equals 4.
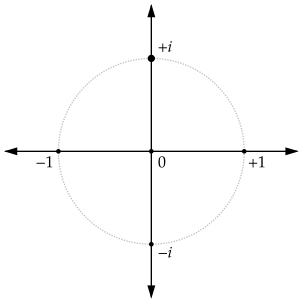
The Square Roots of -1
Normally, when you take the square root of a number, you're looking for a number that, when multiplied by itself, gives you the original number. For example, the square root of 4 is 2 (because 2 times 2 is 4).
But what about the square root of −1? There is no "normal" number that you can multiply by itself to get −1. This is where complex numbers come in!
Mathematicians created a special number called i (the imaginary unit). By definition, i multiplied by i (or i2) equals −1. So, i is a square root of −1. The only other complex number that works is −i.
Using Negative Numbers as Powers
You can also use negative numbers as powers (or exponents). When a number has a power of −1, it means you take its reciprocal.
For example, x−1 is the same as 1 divided by x (written as 1/x). So, 5−1 is 1/5. This rule works for any number that isn't zero.
How Computers Store -1
Computers need a way to store negative numbers like −1. The most common way they do this is using something called "two's complement". This is a clever system that lets computers represent both positive and negative numbers using only ones and zeros.
See also
 In Spanish: Menos uno para niños
In Spanish: Menos uno para niños

