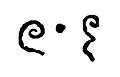Zero facts for kids
Quick facts for kids
|
||||
|---|---|---|---|---|
| Cardinal | 0, zero, "oh", nought, naught, nil, o, 〇 | |||
| Ordinal | 0th (zeroth, noughth) |
|||
| Divisors | all other numbers (except itself) |
|||
| Binary | 02 | |||
| Ternary | 03 | |||
| Senary | 06 | |||
| Octal | 08 | |||
| Duodecimal | 012 | |||
| Hexadecimal | 016 | |||
| Arabic | ٠,0 | |||
| Bengali | ০ | |||
| Devanāgarī | ० | |||
| Chinese | 零, 〇 | |||
| Japanese | 零, 〇 | |||
| Khmer | ០ | |||
| Thai | ๐ | |||
Zero (0) is a very special number. When we say there are zero things, it means there is nothing there. For example, if you have zero hats, it means you do not have any hats at all.
Contents
What is the Symbol for Zero?
The symbol we use for the number zero is "0". Zero is like a special helper in math. When you add zero to any number, that number stays the same. It's like adding nothing!
Doing Math with Zero
Zero acts in unique ways when you use it in math problems. Here are some important rules:
Adding and Subtracting Zero
- Adding zero to a number keeps the number the same.
* Example: 3 + 0 = 3
- Subtracting zero from a number also keeps it the same.
* Example: 3 − 0 = 3
- If you subtract a positive number from zero, the answer becomes negative.
* Example: 0 − 3 = −3
Multiplying and Dividing by Zero
- Multiplying any number by zero always gives zero.
* Example: 43 × 0 = 0
- Dividing zero by any other number (except zero itself) always gives zero.
* Example: 0 ÷ 43 = 0
- You cannot divide any number by zero. The answer is "undefined."
* Example: 43 ÷ 0 has no answer.
- You also cannot divide zero by zero. This also has no answer.
* Example: 0 ÷ 0 has no answer.
Zero in Other Math Operations
Here's a quick look at how zero works in different math operations, where x can be any number:
| Operation | Rule | Example |
|---|---|---|
| Addition | x + 0 = x | 3 + 0 = 3 |
| Subtraction | x - 0 = x | 3 - 0 = 3 |
| Multiplication | x × 0 = 0 | 5 × 0 = 0 |
| Division | 0 ÷ x = 0, when x is not 0 | 0 ÷ 5 = 0 |
| x ÷ 0 is undefined | 5 ÷ 0 is undefined | |
| Powers (Exponentiation) | 0x = 0, when x is not 0 | 05 = 0 |
| x0 = 1, when x is not 0 | 50 = 1 | |
| Square Root | √0 = 0 | |
| Logarithm | logb(0) is undefined | |
| Factorial | 0! = 1 |
The Story of Zero
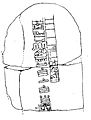
The idea of zero came about in different places around the world at different times. People in Babylon, India, and Central America all thought about zero on their own.
Some places did not have the idea of zero, which made math harder for them. For example, in our calendar, the year after 1 BC is AD 1. There is no year zero in between!
In India, a mathematician named Brahmagupta wrote about zero in the 600s. Over many hundreds of years, the idea of zero traveled from India and Babylon to places like Greece, Persia, and the Arab world. Europeans learned about zero from the Arabs. This is why the numbers we use today are often called "Arabic numerals."
Zero as a Type of Number
Zero is a special kind of number.
- It is a whole number.
- It is not a positive number.
- It is not a negative number.
- It is a neutral number.
When we count down for something, like a rocket launch, we say: "three, two, one, zero (or go)!" Zero is the exact moment the event starts.
Most people, especially mathematicians, agree that zero is a number. If you have a bank account with a balance of zero, it means you have a specific amount of money: none. This is still a quantity, even if it's empty!
The Numeral Zero
The symbol "0" is also called a numerical digit. We use it to show that there are no tens, hundreds, or other place values in a number. This is very important for our number system.
How Zero Helps with Place Value
- In the number 10, the zero shows there is one group of ten and zero single units.
- In the number 100, the zeros show there is one group of a hundred, zero groups of ten, and zero single units.
Without zero, it would be much harder to write large numbers clearly!
Zero (0) vs. the Letter O
The number 0 and the letter O look very similar because they are both round. However, they are different! This difference is very important for computers. A computer cannot do math with the letter O because it expects a number.
Sometimes, people use special ways to write zero so it doesn't get mixed up with the letter O.
- Some computer screens might show zero with a dot in the middle.
- Others might show zero with a slash through it, like a diagonal line.
- On some European car license plates, the zero might be shaped like an egg or have a small opening on one side, while the letter O is more circular. This helps people tell them apart quickly.
When you write by hand, you can add a slash through the zero if you want to make sure it looks different from the letter O.
Zeroes of a Function
In math functions, a "zero" (or "root") is a special input number that makes the function's answer equal to zero.
For example, imagine a function called f(x) = x2 − 1.
- If you put in 1 for x, the answer is 12 − 1 = 1 − 1 = 0.
- If you put in -1 for x, the answer is (-1)2 − 1 = 1 − 1 = 0.
So, 1 and -1 are the "zeroes" of this function.
Finding the zeroes of a function is a way to solve an equation. For example, if you want to solve x2 = 1, you can change it to x2 − 1 = 0. Then, finding the zeroes of the function f(x) = x2 − 1 gives you the solutions to the equation.
Related Pages
Images for kids
-
The back of an ancient stone from Tres Zapotes showing early use of zero.
See also
 In Spanish: Cero para niños
In Spanish: Cero para niños