Brahmagupta facts for kids
Quick facts for kids
Brahmagupta
|
|
|---|---|

Hindu astronomer, 19th-century illustration
|
|
| Born | c. 598 CE |
| Died | c. 668 CE (aged c. 69–70) |
| Known for |
|
| Scientific career | |
| Fields | Astronomy, mathematics |
| Influenced | Virtually all subsequent mathematics particularly Indian and Islamic mathematics |
Brahmagupta (born around 598 CE – died around 668 CE) was a brilliant Indian mathematician and astronomer. He wrote two important books about math and space. One was called Brāhmasphuṭasiddhānta (meaning "correct teachings of Brahma") written in 628 CE. The other was Khaṇḍakhādyaka (meaning "edible bite") from 665 CE.
Brahmagupta was the first person to create clear rules for using the number zero in calculations. He also explained how to work with negative numbers. His books were written in Sanskrit poetry, which was a common way to share knowledge in ancient India.
In 628 CE, Brahmagupta also described gravity as a force that pulls things. He used the Sanskrit word "gurutvākarṣaṇam" to explain this idea.
Contents
Life and work
Brahmagupta was born in 598 CE in a place called Bhillamala, which is now Bhinmal in Rajasthan, India. He lived there during the time of King Vyagrahamukha. Brahmagupta was the son of Jishnugupta and followed the Hindu religion. He spent a big part of his life working in Bhillamala. Later, another scholar called him "Bhillamalacharya," meaning "the teacher from Bhillamala."
Bhillamala was a very important city and a center for learning about math and astronomy. Brahmagupta became an astronomer for the Brahmapaksha school, which was one of the main astronomy schools in India. He studied many older books and the work of other famous astronomers like Aryabhata.
When he was 30 years old, in 628 CE, Brahmagupta wrote his most famous book, the Brāhmasphuṭasiddhānta. Many people believe this was a new and improved version of an older astronomy book. Brahmagupta added many new and original ideas to it. This book has 24 chapters and over 1000 verses. A lot of it is about astronomy, but it also has important parts about math, including algebra, geometry, and how to solve problems step-by-step.
Later, Brahmagupta moved to Ujjain, another big center for astronomy in central India. When he was 67, he wrote his second well-known book, Khandakhadyaka. This book was a practical guide for students learning about Indian astronomy. Brahmagupta passed away in 668 CE, likely in Ujjain.
His books
Brahmagupta wrote these important books:
- Brāhmasphuṭasiddhānta, finished in 628 CE.
- Khaṇḍakhādyaka, finished in 665 CE.
- Grahaṇārkajñāna, (mentioned in one old copy).
Mathematics
Algebra: Solving equations
Brahmagupta was a pioneer in algebra, which is a branch of math that uses letters and symbols to solve problems. He showed how to solve equations like bx + c = dx + e. His solution was similar to what we use today: x = (e − c) / (b − d).
He also gave two ways to solve a more complex type of equation called a quadratic equation. This is an equation where a variable is squared, like ax2 + bx = c.
Brahmagupta also worked on solving problems with many unknown numbers. He suggested using a method he called "the pulverizer" to find solutions.
His algebra was written in a special way, using abbreviations for words instead of full sentences. For example, he put numbers side by side for addition and a dot over a number for subtraction. This was similar to how some ancient Greek mathematicians wrote.
Arithmetic: How we calculate
The basic math operations (adding, subtracting, multiplying, and dividing) were known before Brahmagupta. However, the way we write numbers today, using the Hindu–Arabic numeral system (like 1, 2, 3, 0), first appeared in Brahmagupta's Brāhmasphuṭasiddhānta.
In his book, he described four ways to multiply numbers. He also explained how to work with fractions, showing rules for adding, multiplying, and subtracting them. He even explained how to find the cube and cube-root of a number.
Squares and Cubes
Brahmagupta also found ways to calculate the sum of the squares and cubes of the first few numbers. For example, he showed that the sum of the squares of the first n natural numbers is n(n + 1)(2n + 1) / 6. He also found a formula for the sum of the cubes.
Zero: A number of its own
Brahmagupta's Brāhmasphuṭasiddhānta is the first known book to treat zero as a number, not just a placeholder. Before him, people like the Babylonians used zero to show an empty place, but not as a number you could do math with.
In his book, Brahmagupta gave rules for adding, subtracting, and multiplying with negative numbers and zero. His rules are very similar to what we use today. For example, he said that a negative number plus zero is the negative number, and zero plus a positive number is the positive number.
However, his rule for dividing by zero was different from modern math. He said that zero divided by zero is zero. In modern math, dividing by zero is not allowed or is "undefined."
Geometry: Shapes and spaces
Brahmagupta spent a lot of time on geometry, which is the study of shapes, sizes, and positions of figures.
Brahmagupta's formula
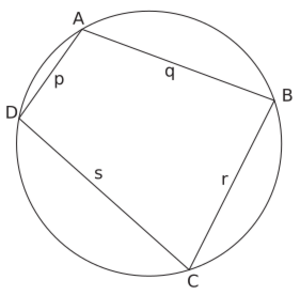
One of his most famous geometry discoveries is his formula for finding the area of a special four-sided shape called a cyclic quadrilateral. This is a shape where all four corners touch a circle.
If you know the lengths of the four sides (let's call them p, q, r, and s), you can find the exact area using his formula. This formula is very important because Heron's formula (for the area of a triangle) is actually a special case of Brahmagupta's formula.
Triangles
Brahmagupta also worked on triangles. He described how to find the lengths of segments created when a height is drawn in a triangle. He also gave a theorem about "rational triangles," which are triangles with sides and areas that can be written as fractions.
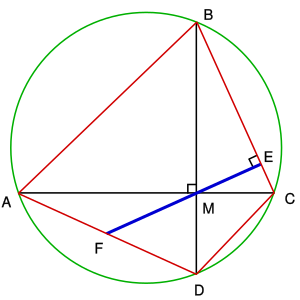
Brahmagupta's theorem
Brahmagupta also had a theorem about cyclic quadrilaterals. It describes a special property of the diagonals (lines connecting opposite corners) when they cross each other.
Pi
Brahmagupta also gave values for Pi (π), which is the ratio of a circle's circumference to its diameter. He said that 3 was a "practical" value for Pi. For a more "accurate" value, he suggested using the square root of 10, which is about 3.1622. This was a very good estimate for his time.
Measurements and constructions
Brahmagupta also explained how to draw different shapes with specific side lengths. He showed how to create triangles, rectangles, and trapezoids using right triangles.
He also worked on finding the volume and surface area of 3D shapes. He found the volume of rectangular boxes, pyramids, and parts of pyramids (called frustums).
Trigonometry: Angles and distances
Brahmagupta also made important contributions to trigonometry, which is used to study relationships between angles and sides of triangles.
Sine table
He created a "sine table," which is a list of values for the sine function at different angles. These tables are used in astronomy and navigation to calculate positions and distances. He used special words to represent numbers in his table, which was a common practice in Sanskrit writings.
Interpolation formula
Brahmagupta also developed a way to find new values for the sine function from values he already had in his table. This method is called an interpolation formula. It helps to estimate a value that falls between two known values. This was a very advanced idea for his time.
Astronomy
Brahmagupta made many important contributions to astronomy. He developed methods for calculating where planets and stars would be at different times. He also showed how to predict when the sun and moon would rise and set, when planets would line up (conjunctions), and when eclipses would happen.
In his Brāhmasphuṭasiddhānta, Brahmagupta explained how the Moon gets its light from the Sun. He showed that because the Moon is closer to Earth than the Sun, the amount of the Moon that looks lit up depends on where the Sun and Moon are compared to each other. This can be figured out by looking at the angle between them.
He also discussed the paths of planets, how the Earth spins, and more about lunar and solar eclipses in his book Khandakhadyaka.
See also
 In Spanish: Brahmagupta para niños
In Spanish: Brahmagupta para niños
- Brahmagupta–Fibonacci identity
- Brahmagupta's formula
- Brahmagupta theorem
- Chakravala method
- List of Indian mathematicians
- History of science and technology in the Indian subcontinent