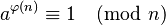Euler's totient theorem facts for kids

Euler's totient theorem, also known as the Fermat–Euler theorem, is a cool idea in number theory. It helps us understand how numbers behave when we divide them and look at the remainder.

This theorem says that if you have two whole numbers, let's call them a and n, and they are coprime, then something special happens. Being coprime means that the only number that can divide both a and n evenly is 1. They don't share any other common factors.

If a and n are coprime, then this mathematical rule is true:

This might look complicated, but let's break it down!

• The symbol 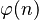is called Euler's totient function. It counts how many positive whole numbers are less than or equal to n and are also coprime to n. For example, if n is 6, the numbers less than or equal to 6 are 1, 2, 3, 4, 5, 6. The numbers coprime to 6 are 1 and 5 (because 2, 3, 4, 6 share factors with 6). So, 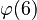Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \varphi(6) would be 2.
• The expression 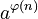Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^{\varphi (n)} means a multiplied by itself 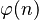Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \varphi (n) times.
• The symbol 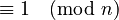Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \equiv 1 \pmod{n} means that when you divide 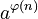Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^{\varphi (n)} by n, the remainder is 1. This is called "modular arithmetic." It's like a clock where numbers "wrap around" after reaching a certain point.

Who Discovered This Theorem?

This important theorem is named after a brilliant Swiss mathematician named Leonhard Euler. He lived in the 1700s and made huge contributions to many areas of mathematics.

Euler's theorem is actually a more general version of an older theorem called Fermat's little theorem. This earlier theorem was published by a French mathematician named Pierre de Fermat in 1640. Fermat's theorem was amazing for its time, but it wasn't fully proven until Euler came along about a hundred years later and proved his more powerful version.

Why Is Euler's Theorem Important?

Euler's totient theorem is super useful in many parts of mathematics, especially in cryptography. Cryptography is the science of making and breaking secret codes. For example, it's used in the RSA encryption system, which helps keep your online information safe when you're shopping or sending messages.

It helps us understand patterns in numbers and how they repeat when we work with remainders. This makes it a powerful tool for solving complex problems in number theory and computer science.

See also

In Spanish: Teorema de Euler para niños