Existence quantifier facts for kids
The existence quantifier is a special symbol used in mathematics and logic. It helps us say that something is true for at least one thing in a group. Think of it like saying, "There is at least one student in this class who likes pizza."
What is the Existence Quantifier?
The existence quantifier is a symbol that looks like a backward "E":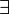 
. We read it as "there exists" or "for some." It tells us that a statement is true for at least one item in a specific collection or group.
For example, if we say "some natural number is equal to 3 + 5," we are using the idea of existence. In math, we could write this as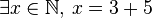 
. This means "there exists a number x in the set of natural numbers such that x equals 3 + 5." Since 8 is a natural number and 3 + 5 = 8, this statement is true!
How It Works
When you see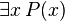 
, it means "there exists an x such that P(x) is true."
- x stands for an item in the group we are talking about.
- P(x) is a statement or condition about x.
This whole statement is true if you can find just one x in the group that makes P(x) true. If you can't find even one, then the statement is false.
Existence vs. Universal Quantifier
It's important to know that the existence quantifier is different from the universal quantifier.
- The existence quantifier (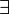) means "there is at least one."
- The universal quantifier (
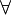, which looks like an upside-down "A") means "this is true for all" or "for every."
For example:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \exists x \in \text{Animals}, x \text{ can fly} (There exists an animal that can fly) is true because birds can fly.
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \forall x \in \text{Animals}, x \text{ can fly} (All animals can fly) is false because not all animals can fly (like dogs or fish).
Understanding these quantifiers helps us be very precise when we talk about groups of things in mathematics and logic.
