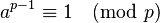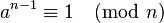Fermat primality test facts for kids

The Fermat primality test is a quick way to guess if a number is a prime number. It's like a first check, but it's not always perfect.

How it Works

This test is based on a cool math rule called Fermat's little theorem. This rule says: if you have a prime number p, and another number a that isn't a multiple of p, then if you multiply a by itself p-1 times, the answer will be 1 when you divide it by p.

In math, we write this as:

This means that 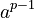Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^{p-1} and 1 have the same remainder when divided by p.

To test if a number n is prime, we pick a random number a (usually between 2 and n-2). Then, we check if the rule holds for n instead of p:

• If this rule does not hold, then we know for sure that n is a composite (not prime). The number a is then called a Fermat witness because it "witnesses" that n is composite.
• If the rule does hold, then n might be prime. We call n a probable prime in this case. However, it's also possible that n is composite, but a just happened to make the rule look true. If this happens, a is called a Fermat liar.

We don't pick a as 1 or n-1 because those numbers always make the rule true, even if n is not prime. So, they don't help us test anything.

Example

Let's try to see if the number 221 is prime.

1. We pick a random number a between 2 and 219. Let's choose a = 38. 2. Now we check the rule: Is 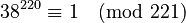Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 38^{220} \equiv 1 \pmod{221} ? * After doing the math, we find that yes, 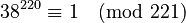Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 38^{220} \equiv 1 \pmod{221} . * This means 221 *might* be prime, or 38 is a Fermat liar.

3. To be more sure, we pick another random number. Let's choose a = 24. 4. Now we check the rule again: Is 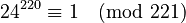Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 24^{220} \equiv 1 \pmod{221} ? * This time, we find that Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 24^{220} \equiv 81 \pmod{221} . * Since 81 is not 1, the rule does not hold!

Because the rule didn't hold for a = 24, we know for sure that 221 is a composite number. It's not prime. In this example, 24 is a Fermat witness, and 38 was a Fermat liar.

How the Test Works (Algorithm)

Here's how you would use this test:

• Input:

* n: The number you want to test (it must be greater than 3). * k: How many times you want to try picking a random a. More tries make the test more reliable.

• Output:

* "composite" if n is definitely not prime. * "probably prime" if n seems to be prime after all the tests.

Here are the steps: 1. Repeat the following k times: * Pick a random number a between 2 and n - 2. * Calculate 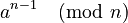Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^{n-1} \pmod n . * If the result is not 1, then n is definitely composite. Stop and say "composite". 2. If you finish all k tries and never found a result that was not 1, then n is probably prime. Say "probably prime".

The Test's Weakness

The Fermat primality test has a weakness: some composite numbers can fool it. These are called Fermat pseudoprimes. For example, 221 is a composite number, but 38 made it look prime.

Even trickier are special numbers called Carmichael numbers. For these numbers, almost *every* choice of a will be a Fermat liar! This means the test will almost always say a Carmichael number is "probably prime," even though it's actually composite. Luckily, Carmichael numbers are quite rare.

Because of these "liars" and "Carmichael numbers," the Fermat test isn't used alone for very important tasks like making sure a number is prime for computer security. Instead, mathematicians and computer scientists use stronger tests like the Miller–Rabin primality test or Baillie–PSW primality test. These tests are much better at telling prime numbers from composite ones.

Where it's Used

Even with its weaknesses, the Fermat test can still be useful. Sometimes, it's used as a very quick first check before running a more powerful test. It's like a quick "sniff test" to see if a number is obviously not prime.

For example, some computer programs that deal with very large numbers, like those used for PGP (a program for secure communication), might use the Fermat test as a fast way to check if a newly generated number is likely prime. If it passes the Fermat test, then a slower, more reliable test is run.

See also

In Spanish: Test de primalidad de Fermat para niños