Gram–Schmidt process facts for kids
The Gram–Schmidt process is a clever method in mathematics that helps us "tidy up" a group of vectors. Imagine you have several arrows pointing in different directions. This process helps you change them into a new set of arrows that are all perfectly perpendicular to each other. It can also make them "orthonormal," meaning they are perpendicular and each have a length of exactly one.
This method is often used in a part of math called linear algebra, which deals with vectors and spaces. It's especially useful in Euclidean space, which is like the normal space we live in, where we can measure distances and angles.
The Gram–Schmidt process takes a group of vectors that are "linearly independent" (meaning they don't just point in the same direction or are simple copies of each other). It then turns them into a new group of vectors that are perpendicular and still "cover" the same space as the original vectors.
The method is named after two mathematicians, Jørgen Pedersen Gram and Erhard Schmidt. However, a very famous mathematician named Pierre-Simon Laplace knew about it even before them!
One important use of the Gram–Schmidt process is in something called QR decomposition. This is a way to break down a matrix (a grid of numbers) into two simpler parts: one that is "orthogonal" (like our perpendicular vectors) and one that is "triangular."
Contents
How the Gram–Schmidt Process Works
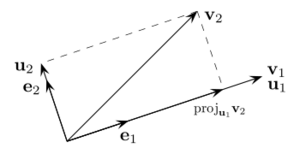
Let's think about how this process works step by step. Imagine you have a set of original vectors, let's call them v1, v2, and so on. The goal is to create a new set of vectors, u1, u2, etc., that are all perpendicular to each other.
First, we pick the first original vector, v1. This will be our first "straightened" vector, so we set u1 = v1.
Next, we want to find u2. We take the second original vector, v2. We then remove any part of v2 that points in the same direction as u1. Think of it like finding the "shadow" of v2 on u1 and then subtracting that shadow. What's left will be perfectly perpendicular to u1. This leftover part becomes u2.
We use a special tool called a "projection operator" for this. It helps us find the part of one vector that lies along another. The formula for this is: 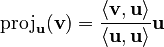 Here,
Here, 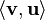 is the "inner product" (like a dot product) of the vectors v and u. It tells us how much they point in the same direction.
is the "inner product" (like a dot product) of the vectors v and u. It tells us how much they point in the same direction.
So, the steps look like this:
- u1 = v1
- u2 = v2 - (the part of v2 that points along u1)
- u3 = v3 - (the part of v3 that points along u1) - (the part of v3 that points along u2)
And so on for all the vectors. Each new u vector is made by taking the original v vector and subtracting all the parts that point along the previously found u vectors. This guarantees that each new u vector is perpendicular to all the ones before it.
Once you have all the u vectors (which are perpendicular), you can make them "orthonormal" by simply dividing each u vector by its own length. This makes each vector have a length of 1. These new vectors are often called e1, e2, etc.
If you apply this process to a set of vectors that are not truly independent (meaning some are just combinations of others), the process will give you a zero vector at some point. If you want an orthonormal set, you just skip these zero vectors. The number of non-zero vectors you end up with tells you the true "dimension" of the space your original vectors covered.
Example in 2D Space
Let's try an example with two vectors in a 2D space (like a flat piece of paper). Our original vectors are:
- v1 = (3, 1)
- v2 = (2, 2)
First, we set u1:
- u1 = v1 = (3, 1)
Next, we find u2. We need to subtract the part of v2 that points along u1. The projection of v2 onto u1 is calculated as: 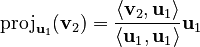 Let's calculate the dot products:
Let's calculate the dot products:
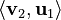 = (2 * 3) + (2 * 1) = 6 + 2 = 8
= (2 * 3) + (2 * 1) = 6 + 2 = 8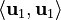 = (3 * 3) + (1 * 1) = 9 + 1 = 10
= (3 * 3) + (1 * 1) = 9 + 1 = 10
So, the projection is: 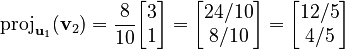
Now, we find u2: 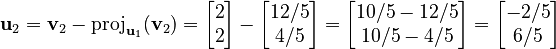
So, our orthogonal vectors are u1 = (3, 1) and u2 = (-2/5, 6/5). We can check if they are perpendicular by calculating their dot product: 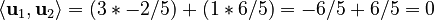 Since the dot product is 0, they are indeed perpendicular!
Since the dot product is 0, they are indeed perpendicular!
To make them orthonormal (length 1), we divide each by its length:
- Length of u1 =
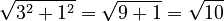
- e1 =
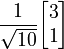
- Length of u2 =
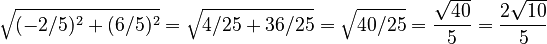
- e2 =
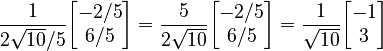
Now we have two orthonormal vectors: e1 and e2.
Numerical Stability
When computers perform the Gram–Schmidt process, tiny "rounding errors" can happen. These errors can make the vectors not perfectly perpendicular, especially if there are many vectors or if the original vectors are almost pointing in the same direction. This is called "numerical instability."
To fix this, there's a slightly different version called the modified Gram-Schmidt (MGS) process. It gives the exact same answer if there are no errors, but it handles the small computer errors much better.
Instead of subtracting all the projections at once, the modified version subtracts them one by one. For example, to find uk, it first subtracts the part along u1, then from that new vector, it subtracts the part along u2, and so on. This step-by-step approach helps keep the vectors more accurately perpendicular.
Algorithm (Computer Steps)
Here's how you might tell a computer to do the classical Gram–Schmidt process, using a language like MATLAB:
function U = gramschmidt(V)
% V is a matrix where each column is an input vector
% U will be a matrix where each column is an orthonormal vector
[n, k] = size(V); % n is dimension of vectors, k is number of vectors
U = zeros(n,k); % Create an empty matrix for the results
% First vector is just the first input vector, normalized
U(:,1) = V(:,1) / norm(V(:,1));
% Loop through the rest of the vectors
for i = 2:k
U(:,i) = V(:,i); % Start with the original vector
% Subtract projections onto all previously found U vectors
for j = 1:i-1
% Calculate the projection and subtract it
U(:,i) = U(:,i) - (U(:,j)'*U(:,i)) * U(:,j);
end
% Normalize the resulting vector
U(:,i) = U(:,i) / norm(U(:,i));
end
endThis set of instructions tells the computer exactly how to perform the Gram–Schmidt orthonormalization. It's a very efficient way to do it for many vectors.
See also
 In Spanish: Proceso de ortogonalización de Gram-Schmidt para niños
In Spanish: Proceso de ortogonalización de Gram-Schmidt para niños