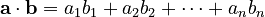Dot product facts for kids

The dot product is a cool math tool that takes two vectors and gives you a single number back. This number tells you something about how long the vectors are and how much they point in the same direction.

Think of vectors like arrows that have both a length and a direction. The dot product helps us understand the relationship between two of these arrows. It's also called the scalar product because the answer you get is a scalar, which is just a plain number, not another vector.

In three-dimensional space, the dot product is different from the cross product. The cross product gives you another vector as an answer, while the dot product always gives you a number.

What is the Dot Product?

The dot product is a way to multiply two vectors. Let's say you have two vectors, a and b.

If a = [a₁, a₂, ..., a_n] and b = [b₁, b₂, ..., b_n], the dot product is found by multiplying their matching parts and then adding all those results together.

Here's how it looks:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathbf{a}\cdot \mathbf{b} = a_1b_1 + a_2b_2 + \cdots + a_nb_n

The n here means how many parts (or dimensions) the vectors have.

Example

Let's try an example with two 3D vectors: [1, 3, −5] and [4, −2, −1].

To find their dot product, we do this:

• Multiply the first parts: 1 × 4 = 4
• Multiply the second parts: 3 × (−2) = −6
• Multiply the third parts: (−5) × (−1) = 5
• Then, add these results together: 4 + (−6) + 5 = 3

So, the dot product of [1, 3, −5] and [4, −2, −1] is 3.

Dot Product in Physics

The dot product is super useful in physics because it helps describe how forces and movements work together. When you use the dot product in physics, the answer is a scalar quantity. This means it's a number with a unit, like "joules" for energy, and it doesn't depend on which way you're looking at it.

Here are some examples:

• Mechanical work: This is the dot product of force and displacement vectors. It tells you how much energy is used when a force moves something a certain distance.
• Magnetic flux: This is the dot product of the magnetic field and the area vectors. It helps measure the total magnetic field passing through a surface.
• Volumetric flow rate: This is the dot product of the fluid velocity and the area vectors. It tells you how much fluid flows through a certain area over time.

Properties of the Dot Product

The dot product has some cool properties that make it easy to work with:

• Order doesn't matter (Commutative)

You can swap the order of the vectors, and the answer will be the same:  :

• It works with addition (Distributive)

If you add two vectors first and then take the dot product with a third, it's the same as taking the dot product with each one separately and then adding those results:  :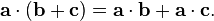

• Multiplying by a number

If you multiply a vector by a number (a scalar) before taking the dot product, it's the same as taking the dot product first and then multiplying the result by that number:  :

• Perpendicular vectors

If two vectors are perpendicular (they form a 90-degree angle), their dot product is always zero. And if their dot product is zero, they must be perpendicular (unless one of them is the zero vector).

Related pages

• Cauchy–Schwarz inequality
• Cross product
• Matrix multiplication

• Want to learn more? Check out these helpful videos: video 1 and video 2 from an online Interactive 3D graphics course.

Images for kids

• 

  This image shows the parts of a vector in a standard coordinate system.

See also

In Spanish: Producto escalar para niños