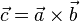Cross product Facts for Kids

The cross product is a special way to combine two vectors in three-dimensional space. Think of a vector as an arrow that has both a length (its size) and a direction. The cross product is often shown with the symbol $\times$ .

When you "cross" two vectors, you get a brand new vector. This new vector is always at a right angle (90 degrees) to both of the original vectors. This is why the cross product is mostly used for vectors in three dimensions.

Why is the Cross Product Important?
Seeing the Cross Product in 3D Space
How to Calculate the Cross Product
- Calculating with Coordinates
- Calculating with Angle and Magnitude
Basic Rules of the Cross Product
Related pages
Images for kids
See also

Why is the Cross Product Important?

The cross product is super useful in many areas of science, especially physics, and also in engineering and mathematics.

For example, it helps us understand:

Torque: This is a twisting force, like when you use a wrench to tighten a bolt. The cross product helps figure out how much twisting force is applied and in what direction.
Magnetic Fields: It's used to describe forces in magnetic fields, which are invisible areas of force around magnets.

Seeing the Cross Product in 3D Space

Finding the direction of the cross product using the right-hand rule.

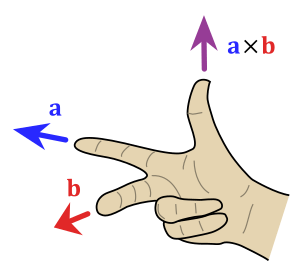
Imagine you have two vectors, let's call them vector a and vector b. When you find their cross product, you get a new vector, let's call it vector c.

\vec{c}=\vec{a} \times \vec{b}

Vector c will always be at a right angle to both vector a and vector b.

To figure out the direction of this new vector c, you can use something called the right-hand rule.

Hold out your right hand.
Point your index finger in the direction of the first vector (vector a).
Point your middle finger in the direction of the second vector (vector b).
Your thumb will then point in the direction of the cross product (vector c).

If the angle between your index and middle fingers is more than 180 degrees, you might need to flip your hand over to make it work.

How to Calculate the Cross Product

You can calculate the cross product of two 3D vectors using their coordinates.

Calculating with Coordinates

Let's say you have two vectors, vector a and vector b, described by their coordinates:

Vector a = 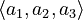Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \langle a_1, a_2, a_3 \rangle (meaning it goes 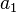$a_1$ units along the x-axis, 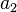$a_2$ along the y-axis, and 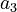Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_3 along the z-axis).
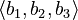
Vector b = Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \langle b_1, b_2, b_3 \rangle

Then, the cross product of vector a and vector b is found using this formula: 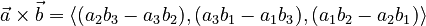Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \vec{a} \times \vec{b} = \langle (a_2 b_3 - a_3 b_2), (a_3 b_1 - a_1 b_3), (a_1 b_2 - a_2 b_1) \rangle

Calculating with Angle and Magnitude

You can also find the cross product if you know the angle between the two vectors and their lengths (called magnitudes).

The formula is: $\vec{a} \times \vec{b} = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin (\theta) \ \mathbf{n}$

Here's what each part means:

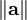Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \left\| \mathbf{a} \right\| is the length (magnitude) of vector a.
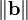Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \left\| \mathbf{b} \right\| is the length (magnitude) of vector b.
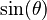Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin (\theta) is the sine of the angle ( 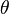$\theta$ ) between vector a and vector b.
n is a special unit vector (a vector with a length of 1) that points in the direction perpendicular to both a and b. Its direction is found using the right-hand rule.

Basic Rules of the Cross Product

The cross product has some interesting rules:

Order Matters: If you switch the order of the vectors, the direction of the new vector flips.

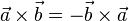
* $\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}$

Distributing: You can "distribute" the cross product over addition, similar to how you do with regular multiplication.

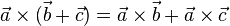
* $\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$

Multiplying by a Number: If you multiply one of the vectors by a number (a scalar), it's the same as multiplying the final cross product by that number.

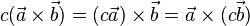
* $c(\vec{a} \times \vec{b}) = (c\vec{a})\times\vec{b} = \vec{a}\times(c\vec{b})$

Images for kids

The cross product a × b (vertical, in purple) changes as the angle between the vectors a (blue) and b (red) changes. The cross product is always at a right angle to both vectors. Its length is zero when the vectors are parallel and largest when they are at a right angle to each other.

Cross product facts for kids

Contents