Cartesian product facts for kids
In mathematics, a Cartesian product is a special way to combine two groups of items, called sets. Imagine you have two different lists of things. The Cartesian product takes every item from the first list and pairs it up with every item from the second list.
For example, if you have a set of colors {red, blue} and a set of sizes {small, large}, the Cartesian product would give you: (red, small), (red, large), (blue, small), (blue, large). Each pair is called an ordered pair, because the order matters. The first item always comes from the first set, and the second item always comes from the second set.
You write the Cartesian product of set A and set B as A × B. It's like making a list of all possible combinations!
Contents
What is a Set?
Before we dive deeper, let's quickly understand what a set is. In math, a set is just a collection of different items. These items are called "elements" or "members" of the set.
For example:
- Set A could be {apple, banana, cherry} – these are fruits.
- Set B could be {dog, cat, bird} – these are pets.
- Set C could be {1, 2, 3, 4, 5} – these are numbers.
Sets usually have curly brackets `{}` around their elements. Each element in a set is unique; you don't list the same item twice.
How Does the Cartesian Product Work?
Let's use a simple example to see how the Cartesian product creates new pairs.
Imagine you have:
- Set A = {1, 2, 3} (these could be different types of ice cream cones)
- Set B = {a, b} (these could be different toppings: 'a' for sprinkles, 'b' for chocolate syrup)
To find A × B, you take each item from Set A and pair it with every item from Set B.
Here's how it looks:
- Take '1' from Set A:
* Pair '1' with 'a' → (1, a) * Pair '1' with 'b' → (1, b)
- Take '2' from Set A:
* Pair '2' with 'a' → (2, a) * Pair '2' with 'b' → (2, b)
- Take '3' from Set A:
* Pair '3' with 'a' → (3, a) * Pair '3' with 'b' → (3, b)
So, the Cartesian product A × B is the new set of all these pairs: 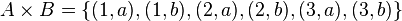
Each pair, like (1, a), is called an "ordered pair." The order matters because (1, a) is different from (a, 1). In a Cartesian product, the first item always comes from the first set you listed (Set A in A × B), and the second item always comes from the second set (Set B).
Visualizing the Cartesian Product
You can think of the Cartesian product as making a grid or a table. Imagine the elements of Set A are the rows and the elements of Set B are the columns. Each box where a row and column meet is one of the ordered pairs.
For example, with A = {1, 2, 3} and B = {a, b}:
| a | b | |
|---|---|---|
| 1 | (1, a) | (1, b) |
| 2 | (2, a) | (2, b) |
| 3 | (3, a) | (3, b) |
This table shows all the possible combinations, which are the elements of the Cartesian product.
Real-World Examples
The Cartesian product helps us understand combinations in everyday life.
Clothing Combinations
Let's say you have:
- Set of shirts (S) = {red shirt, blue shirt}
- Set of pants (P) = {jeans, shorts, khakis}
The Cartesian product S × P would be all your possible outfits:
- (red shirt, jeans)
- (red shirt, shorts)
- (red shirt, khakis)
- (blue shirt, jeans)
- (blue shirt, shorts)
- (blue shirt, khakis)
You can see how many different outfits you can make!
Restaurant Menu Choices
Imagine a simple restaurant menu:
- Set of Main Dishes (M) = {pizza, burger}
- Set of Drinks (D) = {soda, juice, water}
The Cartesian product M × D would show all the possible meal combinations:
- (pizza, soda)
- (pizza, juice)
- (pizza, water)
- (burger, soda)
- (burger, juice)
- (burger, water)
This helps the restaurant know all the choices they offer.
How Many Pairs are There?
A cool thing about the Cartesian product is that you can easily find out how many ordered pairs it will have.
You just multiply the number of elements in the first set by the number of elements in the second set.
- If Set A has 3 elements (like {1, 2, 3})
- And Set B has 2 elements (like {a, b})
Then the Cartesian product A × B will have 3 × 2 = 6 ordered pairs. We saw this in our example: {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)} has 6 pairs!
This is a quick way to check your work or to figure out how many combinations are possible without listing them all.
Related Ideas
The Cartesian product is a basic idea that helps build more complex math concepts. It's used in areas like probability (figuring out chances), statistics (analyzing data), and even in computer science.
Images for kids
See also
 In Spanish: Producto cartesiano para niños
In Spanish: Producto cartesiano para niños


