Vector facts for kids
A vector is a special idea in math that has two main parts: a size (how much there is) and a direction (where it's going). We often show vectors using bold letters like u or v. You can also think of a vector as a line segment that starts at one point and ends at another.
Imagine you're giving directions. If you say, "Walk one kilometer towards the North," that's a vector! It tells you both the distance (one kilometer) and the direction (North). But if you just say, "Walk one kilometer," without saying where to go, that's not a vector. It's called a scalar, which only has a size, not a direction.
We usually draw vectors as arrows. The longer the arrow, the bigger the vector's size. The way the arrow points shows the vector's direction.
Contents
What are some examples of vectors?
Vectors help us describe things that move or have a push/pull in a certain direction.
- When John walks 20 meters north, "north" is the direction and "20 meters" is the size. Together, they form a vector.
- An apple falls down at 10 meters per second. "Down" is the direction, and "10 meters per second" is the speed. This combination is a vector called velocity.
- Displacement is a vector. It tells you how far something moved and in what direction. Just knowing the distance is not enough.
- Force is a vector because it's a push or pull in a specific direction.
- Acceleration is also a vector. It describes how much an object's velocity changes. An object accelerates if its speed changes or if its direction changes.
What are some examples of scalars?
Scalars are simple numbers that only tell you "how much" of something there is, without any direction.
- The distance between two places is 10 kilometers. This is a scalar because it doesn't say "10 kilometers North" or "10 kilometers East."
- The number of fruit in a box is a scalar. It's just a count.
- The length of an object, like a pencil, is a scalar.
- A car driving at 100 kilometers per hour is a scalar (speed). It doesn't tell you where the car is going, just how fast. If you add a direction, like "100 kilometers per hour East," then it becomes a vector (velocity).
How do you add vectors?
Adding vectors is different from adding regular numbers because you have to think about both their size and direction.
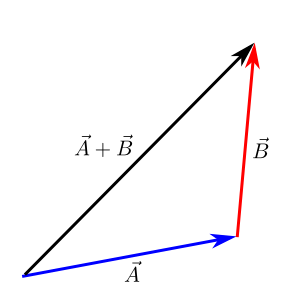
Adding vectors by drawing (Head-to-Tail Method)
The Head-to-Tail method is a cool way to add vectors on paper. It helps you get a good idea of what the final vector will look like.
- First, draw your first vector as an arrow. Make its length match the vector's size (for example, 1 inch could represent 10 meters).
- Next, draw the second vector. Place its "tail" (the starting point of the arrow) at the "head" (the pointy end) of the first vector.
- If you have more vectors, keep doing this: put the tail of the next vector at the head of the one before it.
- Finally, draw a new arrow from the tail of your very first vector to the head of your very last vector. This new arrow is the "resultant" vector, which is the sum of all your vectors!
It's called "Head-to-Tail" because each vector's head connects to the next vector's tail.
Adding vectors using numbers (Component Form)
Sometimes, vectors are described by their "components." Think of components as the x and y (and sometimes z) parts of a vector on a graph.
For example, a vector a might be written as (3, -1). This means it goes 3 units right (or x-direction) and 1 unit down (or y-direction).
To add two vectors using their components, you just add their matching parts: If vector a = (3, -1) And vector b = (2, 2)
To find the sum, vector c, you add the x-parts together and the y-parts together: c = (3 + 2, -1 + 2) c = (5, 1)
This method works for any number of dimensions, not just two!
How do you multiply vectors?
Multiplying vectors can be done in a few ways, and they give different kinds of results.
Multiplying a vector by a scalar (a regular number)
This is the easiest way to multiply a vector. When you multiply a vector by a regular number (a scalar), you just multiply each part of the vector by that number.
For example, if you have a number `c = 5` and a vector x = (3, 4): To find `c` times x, you do: `cx` = (5 times 3, 5 times 4) `cx` = (15, 20)
So, multiplying a vector by a scalar changes its size, and if the scalar is negative, it also flips its direction.
The Dot Product (gives a scalar)
The dot product is one way to multiply two vectors, and the answer you get is always a scalar (a single number, no direction).
Let's say you have vector a = (2, 3) and vector b = (1, 4). To find their dot product (written as a ⋅ b), you multiply the first parts together, multiply the second parts together, and then add those results: a ⋅ b = (2 times 1) + (3 times 4) a ⋅ b = 2 + 12 a ⋅ b = 14
The dot product is useful in physics, for example, to calculate work done by a force.
The Cross Product (gives another vector)
The cross product is another way to multiply two vectors, but this time, the answer you get is another vector! This new vector is at right angles to both of the original vectors.
The cross product is a bit more complex and is often used in 3D space. It's written as a × b.
Related pages
