Gödel numbering Facts for Kids

Imagine you have a secret code where every letter, symbol, and even whole sentences in a special language gets its own unique number. This special way of giving numbers to things is called a Gödel numbering, and the number itself is a Gödel number. A smart mathematician named Kurt Gödel came up with this idea in the 1930s. He used it to prove some really important things about math, called his incompleteness theorems.

Think of it like a special way to 'encode' or turn math symbols and statements into numbers. Once symbols become numbers, a whole sequence of symbols (like a math formula) can also become one big number. This makes it easier to study and work with math ideas using only numbers. Since Gödel shared his idea in 1931, the term "Gödel numbering" is now used for any way of giving numbers to mathematical objects.

What is a Gödel Number?
How Gödel's Encoding Works
- An Example of Gödel Numbering
Many Ways to Number
How Gödel Numbering is Used
More General Uses
See also

What is a Gödel Number?

Kurt Gödel realized that every statement or idea in a math system could be turned into a unique number. This number is its Gödel number. The cool part is that if you know a statement's Gödel number, you can figure out things about the statement itself. For example, if a statement is true or false, its Gödel number might have a special property.

The numbers can be very, very large, but that's okay! The main idea is that such numbers can always be created. It's like a special code where you can always change a math formula into a number and then change the number back into the formula.

A simple example of this idea is how computers store English words. They use something called ASCII. Each letter or symbol gets a number. For instance, the word foxy can be turned into a long number by combining the ASCII codes for each letter:

The word foxy becomes 102111120121.
A math formula like x=y => y=x becomes 120061121032061062032121061120.

How Gödel's Encoding Works

Gödel's original encoding

								number variables				property variables			...
Symbol	0	s	¬	∨	∀	(	)	x₁	x₂	x₃	...	P₁	P₂	P₃	...
Number	1	3	5	7	9	11	13	17	19	23	...	289	361	529	...

Gödel used a clever system based on prime factorization. First, he gave a unique number to every basic symbol in the math language he was working with. For example, the symbol "0" might get the number 1, and the symbol "s" might get the number 3.

To turn a whole formula (which is a sequence of symbols) into a single Gödel number, he used prime numbers. Imagine you have a sequence of numbers like (x₁, x₂, x₃, ..., x_n). The Gödel number for this sequence is found by multiplying the first n prime numbers, each raised to the power of its corresponding number in the sequence:

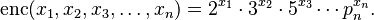
$\mathrm{enc}(x_1,x_2,x_3,\dots,x_n) = 2^{x_1}\cdot 3^{x_2}\cdot 5^{x_3}\cdots p_n^{x_n}.$

This works because of something called the fundamental theorem of arithmetic. This theorem says that any number can be broken down into a unique set of prime numbers multiplied together. So, if you have a Gödel number, you can always work backward to find the original sequence of numbers, and thus the original math formula.

Gödel used this method in two ways:

First, to turn sequences of symbols into numbers (representing formulas).
Second, to turn sequences of formulas into numbers (representing proofs).

This allowed him to connect statements about numbers with statements about whether math theorems could be proven. This was a key idea for his famous proofs.

An Example of Gödel Numbering

Let's look at an example from a specific Gödel numbering system. In this system, the Gödel number for the symbol "0" is 6, and for the symbol "=" is 5.

To find the Gödel number for the formula "0 = 0", we use the prime numbers:

The first symbol is "0", which has the number 6.
The second symbol is "=", which has the number 5.
The third symbol is "0", which has the number 6.

So, the Gödel number for "0 = 0" would be: 2⁶ × 3⁵ × 5⁶ = 64 × 243 × 15625 = 243,000,000.

Many Ways to Number

There isn't just one way to create a Gödel numbering. You can make many different ones! For example, if you have 1000 basic symbols, you could assign each symbol a unique number from 0 to 999. Then, a formula could be seen as a number in a base-1000 system.

This means that each formula could actually be its own Gödel number, just written in a special number system!

How Gödel Numbering is Used

Once a Gödel numbering is set up for a math theory, every rule for making new statements in that theory can be shown as a function that works on natural numbers. If you have a rule that says formula C comes from formulas A and B, then there's a math function that takes the Gödel numbers of A and B and gives you the Gödel number of C.

This is true for Gödel's original numbering and for any other numbering where you can get the original formula back from its Gödel number.

This clever trick allowed Gödel to make statements about a math theory using only numbers. He could then use these number statements to prove important things about whether math systems are consistent (don't have contradictions) and complete (can prove every true statement).

More General Uses

In the study of computability theory (which is about what computers can and can't do), the term "Gödel numbering" is used more broadly. It can mean:

Any way of assigning numbers to parts of a formal language so that a computer program can work with these numbers to do things with the language.
More generally, assigning numbers to elements of any countable mathematical object (like a group of numbers) so that a computer program can work with them.

Sometimes, "Gödel numbering" is even used when the "numbers" are actually strings of characters, especially when talking about how Turing machines (a model of computation) work with strings.

Gödel numbering facts for kids

Contents