Happy ending problem facts for kids
The "happy ending problem" is a cool idea in mathematics. It got its name because it led to the marriage of two mathematicians, George Szekeres and Esther Klein.
The problem asks: If you have five points on a flat surface, and no three of them are in a straight line (this is called "general position"), can you always find four of those points that form a convex quadrilateral? A convex shape means all its corners point outwards, like a regular square or a rectangle. The answer is yes! You can always find such a quadrilateral.
This problem was one of the first ideas that helped create a field of math called Ramsey theory. Ramsey theory looks for patterns that must appear in large enough collections of things.
You can prove the "happy ending problem" by looking at different situations. For example, if four or more points make up the outer shape (called the convex hull), you can just pick any four of them. If the outer shape is a triangle with two points inside it, you can pick the two inner points and one side of the triangle to form your convex quadrilateral.
There's also a bigger idea called the Erdős–Szekeres conjecture. This idea tries to figure out the smallest number of points needed to guarantee a convex polygon with a certain number of sides. For example, for a convex shape with N sides, they guessed you'd need `1 + 2^(N-2)` points. This guess hasn't been fully proven yet, but it's a big challenge in math!
Bigger Polygons
Mathematicians Paul Erdős and George Szekeres proved something even more general. They showed that if you have a very large group of points (again, no three in a straight line), you can always find a group of N points that form a convex polygon, no matter how big N is. This means if you have enough points, you're guaranteed to find a convex triangle, a convex square, a convex pentagon, and so on.
Let's say `f(N)` is the smallest number of points you need to guarantee a convex polygon with N sides. We know some of these numbers:
- `f(3) = 3`: You need at least 3 points to make a triangle.
- `f(4) = 5`: You need at least 5 points to guarantee a convex quadrilateral (this is the happy ending problem!).
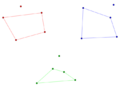
- `f(5) = 9`: You need at least 9 points to guarantee a convex pentagon. The picture shows 8 points that don't make a convex pentagon, so you definitely need more than 8.
- `f(6) = 17`: You need at least 17 points to guarantee a convex hexagon.
For shapes with more than 6 sides, we don't know the exact value of `f(N)` yet. But we do know that `f(N)` is always a real number, meaning you'll always find such a polygon if you have enough points.
Based on the numbers they found, Erdős and Szekeres made a guess (a conjecture) that `f(N)` is always `1 + 2^(N-2)`. They proved that `f(N)` must be at least this big, but proving it's not bigger is still a puzzle for mathematicians!
Empty Convex Polygons
Another interesting question is about "empty" convex polygons. An "empty" polygon means it doesn't have any other points from the original set inside it.
The solution to the happy ending problem also shows that any five points in general position will have an empty convex quadrilateral. Also, any ten points in general position will have an empty convex pentagon.
However, it gets trickier for larger shapes. There are very large sets of points that don't contain any empty convex heptagon (a 7-sided shape).
For a long time, mathematicians wondered if there were always empty convex hexagons (6-sided shapes) in large enough sets of points. Finally, in 2007 and 2008, two mathematicians, Nicolás and Gerken, proved that if you have enough points, you will always find an empty convex hexagon! We know you need at least 30 points to guarantee an empty convex hexagon.
Related Math Problems
This problem is connected to other areas of math. For example, finding sets of points that make the fewest convex quadrilaterals is like trying to draw a complete graph (where every point is connected to every other point) with the fewest lines crossing each other.
The ideas from the happy ending problem can also be used in higher dimensions, not just on a flat surface. In 3D space, for example, if you have enough points, you can find a subset of points that form a convex polytope (a 3D shape with flat sides). These kinds of problems help mathematicians understand how points and shapes behave in different spaces.
Images for kids
-
The happy ending problem: every set of five points in general position contains the vertices of a convex quadrilateral
See also
In Spanish: Problema del final feliz para niños
