Heaviside Function facts for kids

This graph shows the Heaviside step function. It's zero for negative numbers and one for positive numbers.

The Heaviside function, often written as H(x), is a special function in mathematics. Think of it like a switch! Its value is zero for any number smaller than zero (negative numbers). But for any number zero or larger (positive numbers), its value becomes one.

This function is super useful in control theory. It helps describe things that suddenly turn on at a certain moment and then stay on forever. For example, imagine a light switch that turns on a lamp. The Heaviside function can model that sudden change. It was named after an Englishman named Oliver Heaviside, who was a brilliant scientist.

How the Heaviside Function Works

The main idea of the Heaviside function is simple:

• If you give it a negative number (like -5 or -0.1), the function gives you back 0.
• If you give it a positive number (like 3 or 100), the function gives you back 1.

It's like a gate that opens only when the input reaches a certain point.

What Happens at Zero?

What about when the input is exactly zero? This is a bit tricky! The value of the Heaviside function at zero (H(0)) can be defined in different ways depending on what you need it for.

• Sometimes, people say H(0) is 0.
• Sometimes, people say H(0) is 1.
• Often, it's defined as ½ (one half). This makes it a smooth transition between 0 and 1.

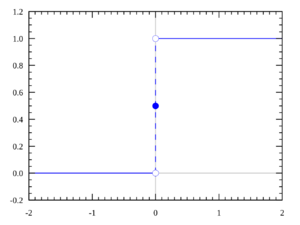
Here's how it looks when H(0) is ½:

• If x is less than 0, H(x) = 0
• If x is exactly 0, H(x) = ½
• If x is greater than 0, H(x) = 1

Related Ideas

• Step function: The Heaviside function is a type of step function, which means it changes its value in sudden "steps."
• Laplace transform: This is a mathematical tool that often uses the Heaviside function to solve problems in engineering and physics.