Regular polygon facts for kids
In geometry, a regular polygon is a special type of polygon. What makes it special? It has two main features:
- All its sides are the same length (this is called equilateral).
- All its angles are the same size (this is called equiangular).
Think of a square or a stop sign (which is an octagon). These are perfect examples of regular polygons!
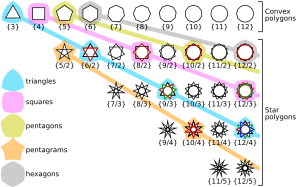
Regular polygons can be either convex or star. A convex polygon bulges outwards, like a normal square or triangle. A star polygon has points that go inwards and outwards, like a five-pointed star.
If you imagine a regular polygon with more and more sides, it starts to look more and more like a circle. If you keep adding sides forever, it would eventually become a perfect circle!
Contents
What Makes Regular Polygons Special?
Regular polygons have some cool properties that are always true, whether they are convex or star-shaped.
Symmetry and Circles
- Rotational Symmetry: A regular polygon with n sides has n-fold rotational symmetry. This means you can turn it around its center n times, and it will look exactly the same each time before it completes a full circle. For example, a square (4 sides) looks the same if you turn it 90 degrees.
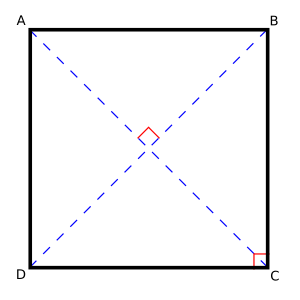
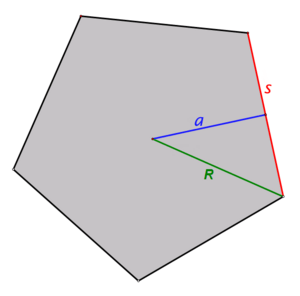
- Circumscribed Circle: All the corners (called vertices) of a regular polygon always lie on a single circle. This circle is called the circumscribed circle. It's like you can draw a circle that perfectly touches every corner of the polygon.
- Inscribed Circle: Because all sides are the same length, every regular polygon also has a circle that fits perfectly inside it. This circle, called the inscribed circle, touches the middle of every side.
Building Regular Polygons
You can draw some regular polygons using only a compass and a straightedge (a ruler without markings). This is possible if the number of sides has special prime factors called Fermat primes. For example, you can draw a regular triangle (3 sides), a square (4 sides), or a pentagon (5 sides) this way. But you can't draw a regular heptagon (7 sides) with just a compass and straightedge.
Images for kids
See also
 In Spanish: Polígono regular para niños
In Spanish: Polígono regular para niños