Infimum and supremum facts for kids
In mathematics, the infimum (say "in-fee-mum") and supremum (say "soo-pray-mum") are special numbers related to a set of other numbers. Think of them as the "tightest" boundaries for a group of numbers. The infimum is the biggest number that is still smaller than or equal to every number in the set. The supremum is the smallest number that is still bigger than or equal to every number in the set. These ideas are very important in a part of mathematics called mathematical analysis.
What are Bounds?
Before we talk about infimum and supremum, let's understand "bounds." Imagine you have a group of numbers.
- A lower bound is any number that is smaller than or equal to all the numbers in your set. For example, if your set is {5, 10, 15}, then 1, 2, 3, 4, and 5 are all lower bounds.
- An upper bound is any number that is bigger than or equal to all the numbers in your set. For the set {5, 10, 15}, numbers like 15, 16, 20, or 100 are all upper bounds.
Understanding Infimum
The infimum is also called the greatest lower bound. It's the largest number among all the lower bounds of a set. It's like finding the highest floor you can stand on that is still below or at the level of all the numbers in your set. If a set has an infimum, it's unique, meaning there's only one. We write it as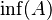 
for a set A.
Understanding Supremum
The supremum is also called the least upper bound. It's the smallest number among all the upper bounds of a set. Think of it as finding the lowest ceiling you can build that is still above or at the level of all the numbers in your set. Like the infimum, if a set has a supremum, it's unique. We write it as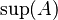 
for a set A.
An Example
Let's look at an example to make this clearer. Imagine a set of numbers A that looks like this: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A = \{ \tfrac{1}{1}, \tfrac{1}{2}, \tfrac{1}{3}, \tfrac{1}{4}, \ldots \} This means the numbers in the set are 1, 0.5, 0.333..., 0.25, and so on. The numbers keep getting smaller and smaller, but they never quite reach zero.
- For this set, the infimum is 0. Even though 0 is not in the set, it's the greatest number that is still less than or equal to every number in the set. The numbers get infinitely close to 0 but never go below it.
- The supremum for this set is 1. This is the smallest number that is greater than or equal to every number in the set. The number 1 is also the first number in the set.
Related Ideas
Infimum and supremum are similar to the maximum and minimum values of a set, but they are more powerful. A set might not have a maximum or minimum value (for example, if it goes on forever or has "holes"), but it can still have an infimum or supremum.
