Integer factorization facts for kids
In number theory, integer factorization is like breaking down a big number into smaller numbers that multiply together to make it. Imagine you have the number 12. You can factor it into 3 and 4, because 3 × 4 = 12.
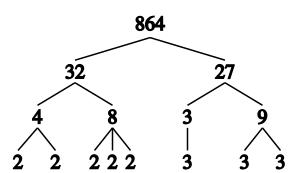
When we only use prime numbers as the smaller parts, it's called prime factorization. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (like 2, 3, 5, 7). So, for 12, its prime factorization would be 2 × 2 × 3.
For very large numbers, finding these factors is incredibly difficult for regular computers. This difficulty is super important for keeping online information safe. Many secret codes, like those used in RSA public-key encryption (which protects your messages and online shopping), rely on the idea that factoring huge numbers is almost impossible.
In 2019, a team of experts factored a 240-digit number (called RSA-240). It took them about 900 years of computer time! They think a slightly bigger number, 1024-bits long, would take 500 times longer.
Not all big numbers are equally hard to factor. The trickiest ones are usually made by multiplying just two very large prime numbers together. If these two prime numbers are similar in size, it makes the problem even harder.
Contents
Prime Factors: The Building Blocks of Numbers
Every positive whole number (except 1) has a unique set of prime factors. This is a fundamental rule in math! Think of prime numbers as the basic building blocks for all other numbers.
It's pretty easy to check if a number is prime or not. There are fast tests for that. But if a number isn't prime (meaning it's a composite number), these tests don't tell you what its factors are. Finding those factors is the hard part.
If you have a way to factor any number, you can keep breaking it down until you only have prime numbers left. For example, if you factor 100 into 10 × 10, you can then factor each 10 into 2 × 5. So, the prime factors of 100 are 2 × 2 × 5 × 5.
Why Factoring is So Hard
Factoring very large numbers is one of the toughest problems in computer science. No one has found a super-fast way for regular computers to factor all numbers. Scientists suspect such a fast method doesn't exist for classical computers.
The best known method for factoring very large numbers on regular computers is called the general number field sieve. It works, but it takes an incredibly long time for huge numbers.
However, there's a special type of computer called a quantum computer. In 1994, a scientist named Peter Shor created an amazing algorithm (a set of instructions for a computer) called Shor's algorithm. This algorithm could factor numbers much, much faster than any known method on a regular computer. If quantum computers become powerful enough, they could break many of the secret codes we use today.
How Computers Try to Factor Numbers
There are different ways computers try to factor numbers. They fall into two main groups:
Special-Purpose Algorithms
These algorithms work best for numbers that have certain features, like having a very small prime factor. They are often used first to try and find any easy factors.
- Trial division: This is like trying to divide a number by every small prime number (2, 3, 5, 7, etc.) until you find a factor.
- Pollard's rho algorithm: A clever method that tries to find factors faster than trial division, especially for numbers with smaller factors.
- Fermat's factorization method: This method works well if a number has two factors that are very close to each other.
General-Purpose Algorithms
These algorithms work for any large number, no matter its special features. They are the ones used to factor the huge numbers in cryptography.
- Quadratic sieve: This was one of the fastest general-purpose methods before the number field sieve.
- General number field sieve: This is currently the fastest known method for factoring very large numbers on regular computers.
Quantum Computer Algorithms
- Shor's algorithm: This is the revolutionary algorithm for quantum computers that could factor numbers much faster than any classical computer.
See also
- Aurifeuillean factorization
- Bach's algorithm for generating random numbers with their factorizations
- Canonical representation of a positive integer
- Factorization
- Multiplicative partition
-adic valuation- Partition (number theory) – a way of writing a number as a sum of positive integers.
