The Iñupiaq language is spoken by the Iñupiat people, who live in Alaska and parts of Canada. Like many languages, Iñupiaq has its own way of counting. What's special about their numbers is that they use a vigesimal system. This means they count in groups of 20, instead of our usual groups of 10 (which is called a decimal system).
Imagine counting on your fingers and toes! That's how a base-20 system works. The Iñupiaq numbers are often written using special symbols called Kaktovik numerals. These symbols were created by students in Kaktovik, Alaska, to make it easier to write Iñupiaq numbers. They match the Iñupiaq words for numbers very well.
How Iñupiaq Numbers Work
The Iñupiaq counting system is based on groups of 20. This is different from the system we use every day, which is based on groups of 10. In Iñupiaq, you'll see numbers built by adding or multiplying by 20.
For example, to say 40, they might say "two twenties." To say 400, they might say "twenty twenties." This makes their number system very logical once you understand the pattern.
Numbers from 0 to 20
The first 20 numbers are the building blocks of the Iñupiaq system. You'll notice some numbers are made by adding or subtracting from 5, 10, or 15. For instance, 7 is "5 plus 2," and 9 is "10 minus 1."
The Kaktovik numerals are a special set of symbols that represent these numbers. They make it easy to write down Iñupiaq numbers, even large ones.
Units (n × 200)
| Numeral |
Morphological
composition |
Kaktovik
notation |
Hindu-Arabic
notation |
| kisitchisaġvik |
|
 |
0 |
| atausiq |
1 |
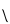 |
1 |
| malġuk |
2 |
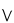 |
2 |
| piŋasut |
3 |
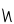 |
3 |
| sisamat |
4 |
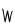 |
4 |
| tallimat |
5 |
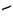 |
5 |
| itchaksrat |
6 |
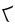 |
6 |
| tallimat malġuk |
5 + 2 |
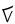 |
7 |
| tallimat piŋasut |
5 + 3 |
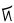 |
8 |
| quliŋŋuġutaiḷaq |
10 − 1 |
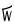 |
9 |
| qulit |
10 |
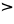 |
10 |
| qulit atausiq |
10 + 1 |
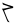 |
11 |
| qulit malġuk |
10 + 2 |
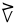 |
12 |
| qulit piŋasut |
10 + 3 |
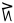 |
13 |
| akimiaġutaiḷaq |
15 − 1 |
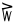 |
14 |
| akimiaq |
15 |
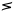 |
15 |
| akimiaq atausiq |
15 + 1 |
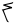 |
16 |
| akimiaq malġuk |
15 + 2 |
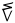 |
17 |
| akimiaq piŋasut |
15 + 3 |
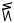 |
18 |
| iñuiññaġutaiḷaq |
20 − 1 |
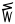 |
19 |
| iñuiññaq |
20 |
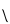  |
20 |
| iḷagiññaq |
400 |
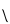   |
400 |
Counting by Twenties (n-kipiaq)
Once you get past 20, the Iñupiaq system uses multiples of 20. The suffix -kipiaq means "times 20." So, malġukipiaq means "two times twenty," which is 40. This pattern continues for higher numbers.
n-kipiaq (n × 201)
| malġukipiaq |
2×20 |
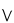  |
40 |
| piŋasukipiaq |
3×20 |
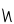  |
60 |
| sisamakipiaq |
4×20 |
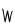  |
80 |
| tallimakipiaq |
5×20 |
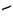  |
100 |
| (tallimakipiaq iñuiññaq) |
5×20 + 20 |
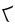  |
120 |
| (tallimakipiaq sisamakipiaq) |
5×20 + 4×20 |
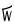  |
180 |
| qulikipiaq |
10×20 |
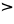  |
200 |
| akimiakipiaq |
15×20 |
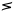  |
300 |
iñuiññakipiaq
(= iḷagiññaq) |
20×20 |
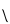   |
400 |
Counting by Four Hundreds (n-agliaq)
The next big step in Iñupiaq counting is 400. This is because 400 is 20 times 20 (202). The suffix -agliaq is used for these numbers. So, malġuagliaq means "two times four hundred," which is 800.
n-agliaq (n × 202)
| malġuagliaq |
2×202 |
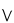   |
800 |
| piŋasuagliaq |
3×202 |
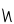   |
1,200 |
| sisamaagliaq |
4×202 |
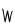   |
1,600 |
| tallimaagliaq |
5×202 |
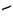   |
2,000 |
| quliagliaq |
10×202 |
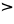   |
4,000 |
| akimiagliaq |
15×202 |
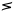   |
6,000 |
Counting by Eight Thousands (n-pak)
When you reach 8,000, you're looking at 20 x 20 x 20 (203). The Iñupiaq word for this is -pak. So, atausiqpak means "one times eight thousand," which is 8,000. This shows how the system keeps building on powers of 20.
n-pak (n × 203)
| atausiqpak |
1×203 |
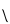 , ,   |
8,000 |
| malġuqpak |
2×203 |
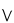 , ,   |
16,000 |
| piŋasuqpak |
3×203 |
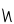 , ,   |
24,000 |
| sisamaqpak |
4×203 |
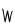 , ,   |
32,000 |
| tallimaqpak |
5×203 |
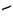 , ,   |
40,000 |
| quliqpak |
10×203 |
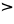 , ,   |
80,000 |
| akimiaqpak |
15×203 |
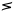 , ,   |
120,000 |
| iñuiññaqpak |
20×203 |
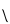  , ,   |
160,000 |
Larger Numbers: Beyond Eight Thousands
The Iñupiaq number system continues to grow by multiplying by 20. You'll see combinations like -kipiaq-pak (20 x 203) and -agliaq-pak (202 x 203). This shows how flexible and powerful a base-20 system can be for expressing very large numbers.
n-kipiaq-pak (n × 204)
| malġukipiaqpak |
2×20×203 |
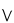  , ,   |
320,000 |
| piŋasukipiaqpak |
3×20×203 |
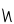  , ,   |
480,000 |
| sisamakipiaqpak |
4×20×203 |
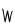  , ,   |
640,000 |
| tallimakipiaqpak |
5×20×203 |
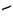  , ,   |
800,000 |
| qulikipiaqpak |
10×20×203 |
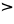  , ,   |
1,600,000 |
| akimiakipiaqpak |
15×20×203 |
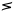  , ,   |
2,400,000 |
n-pak (n × 203)
| iḷagiññaqpak |
400×203 |
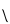   , ,   |
3,200,000 |
n-agliaq-pak (n × 205)
| malġuagliaqpak |
2×202×203 |
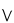   , ,   |
6,400,000 |
| piŋasuagliaqpak |
3×202×203 |
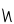   , ,   |
9,600,000 |
| sisamaagliaqpak |
4×202×203 |
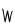   , ,   |
12,800,000 |
| tallimaagliaqpak |
5×202×203 |
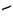   , ,   |
16,000,000 |
| quliagliaqpak |
10×202×203 |
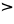   , ,   |
32,000,000 |
| akimiagliaqpak |
15×202×203 |
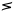   , ,   |
48,000,000 |
n-pakaippaq (n × 206)
| atausiqpakaippaq |
1×(203)2 |
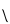 , ,   , ,   |
64,000,000 |
| malġuqpakaippaq |
2×(203)2 |
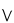 , ,   , ,   |
128,000,000 |
| piŋasuqpakaippaq |
3×(203)2 |
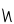 , ,   , ,   |
192,000,000 |
| sisamaqpakaippaq |
4×(203)2 |
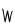 , ,   , ,   |
256,000,000 |
| tallimaqpakaippaq |
5×(203)2 |
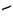 , ,   , ,   |
320,000,000 |
| quliqpakaippaq |
10×(203)2 |
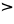 , ,   , ,   |
640,000,000 |
| akimiaqpakaippaq |
15×(203)2 |
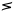 , ,   , ,   |
960,000,000 |
| iñuiññaqpakaippaq |
20×(203)2 |
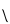  , ,   , ,   |
1,280,000,000 |
n-kipiaq-pakaippaq (n × 207)
| malġukipiaqpakaippaq |
2×20×(203)2 |
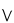  , ,   , ,   |
2,560,000,000 |
| piŋasukipiaqpakaippaq |
3×20×(203)2 |
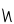  , ,   , ,   |
3,840,000,000 |
| sisamakipiaqpakaippaq |
4×20×(203)2 |
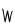  , ,   , ,   |
5,120,000,000 |
| tallimakipiaqpakaippaq |
5×20×(203)2 |
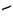  , ,   , ,   |
6,400,000,000 |
| qulikipiaqpakaippaq |
10×20×(203)2 |
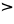  , ,   , ,   |
12,800,000,000 |
| akimiakipiaqpakaippaq |
15×20×(203)2 |
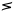  , ,   , ,   |
19,200,000,000 |
n-pakaippaq (n × 206)
| iḷagiññaqpakaippaq |
400×(203)2 |
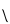   , ,   , ,   |
25,600,000,000 |
n-agliaq-pakaippaq (n × 208)
| malġuagliaqpakaippaq |
2×202×(203)2 |
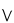   , ,   , ,   |
51,200,000,000 |
| piŋasuagliaqpakaippaq |
3×202×(203)2 |
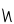   , ,   , ,   |
76,800,000,000 |
| sisamaagliaqpakaippaq |
4×202×(203)2 |
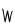   , ,   , ,   |
102,400,000,000 |
| tallimaagliaqpakaippaq |
5×202×(203)2 |
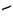   , ,   , ,   |
128,000,000,000 |
| quliagliaqpakaippaq |
10×202×(203)2 |
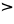   , ,   , ,   |
256,000,000,000 |
| akimiagliaqpakaippaq |
15×202×(203)2 |
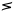   , ,   , ,   |
384,000,000,000 |
n-pakpiŋatchaq (n × 209)
| atausiqpakpiŋatchaq |
1×(203)3 |
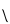 , ,   , ,   , ,   |
512,000,000,000 |
| malġuqpakpiŋatchaq |
2×(203)3 |
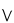 , ,   , ,   , ,   |
1,024,000,000,000 |
| piŋasuqpakpiŋatchaq |
3×(203)3 |
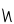 , ,   , ,   , ,   |
1,536,000,000,000 |
| sisamaqpakpiŋatchaq |
4×(203)3 |
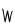 , ,   , ,   , ,   |
2,048,000,000,000 |
| tallimaqpakpiŋatchaq |
5×(203)3 |
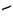 , ,   , ,   , ,   |
2,560,000,000,000 |
| quliqpakpiŋatchaq |
10×(203)3 |
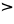 , ,   , ,   , ,   |
5,120,000,000,000 |
| akimiaqpakpiŋatchaq |
15×(203)3 |
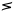 , ,   , ,   , ,   |
7,680,000,000,000 |
| iñuiññaqpakpiŋatchaq |
20×(203)3 |
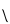  , ,   , ,   , ,   |
10,240,000,000,000 |
n-kipiaq-pakpiŋatchaq (n × 2010)
| malġukipiaqpakpiŋatchaq |
2×20×(203)3 |
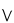  , ,   , ,   , ,   |
20,480,000,000,000 |
| piŋasukipiaqpakpiŋatchaq |
3×20×(203)3 |
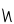  , ,   , ,   , ,   |
30,720,000,000,000 |
| sisamakipiaqpakpiŋatchaq |
4×20×(203)3 |
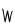  , ,   , ,   , ,   |
40,960,000,000,000 |
| tallimakipiaqpakpiŋatchaq |
5×20×(203)3 |
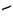  , ,   , ,   , ,   |
51,200,000,000,000 |
| qulikipiaqpakpiŋatchaq |
10×20×(203)3 |
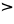  , ,   , ,   , ,   |
102,400,000,000,000 |
| akimiakipiaqpakpiŋatchaq |
15×20×(203)3 |
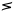  , ,   , ,   , ,   |
153,600,000,000,000 |
n-pakpiŋatchaq (n × 209)
| iḷagiññaqpakpiŋatchaq |
400×(203)3 |
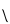   , ,   , ,   , ,   |
204,800,000,000,000 |
n-agliaq-pakpiŋatchaq (n × 2011)
| malġuagliaqpakpiŋatchaq |
2×202×(203)3 |
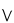   , ,   , ,   , ,   |
409,600,000,000,000 |
| piŋasuagliaqpakpiŋatchaq |
3×202×(203)3 |
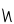   , ,   , ,   , ,   |
614,400,000,000,000 |
| sisamaagliaqpakpiŋatchaq |
4×202×(203)3 |
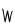   , ,   , ,   , ,   |
819,200,000,000,000 |
| tallimaagliaqpakpiŋatchaq |
5×202×(203)3 |
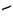   , ,   , ,   , ,   |
1,024,000,000,000,000 |
| quliagliaqpakpiŋatchaq |
10×202×(203)3 |
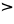   , ,   , ,   , ,   |
2,048,000,000,000,000 |
| akimiagliaqpakpiŋatchaq |
15×202×(203)3 |
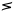   , ,   , ,   , ,   |
3,072,000,000,000,000 |
| iñuiññagliaqpakpiŋatchaq |
20×202×(203)3 |
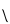 , ,   , ,   , ,   , ,   |
4,096,000,000,000,000 |

