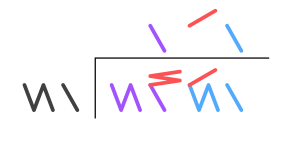Kaktovik numerals facts for kids

The 20 digits of the Kaktovik system

The Kaktovik numerals are a special set of numbers created by the Iñupiat people in Alaska. They are unique because they use a base-20 system, which means they count in groups of 20, unlike our usual base-10 system that counts in groups of 10. These numbers look like pictures, with shapes that show what number they stand for.

The Iñupiaq language and other Eskimo–Aleut languages in Alaska and Canada naturally use a base-20 way of counting. However, the Arabic numerals (the numbers we use every day, like 1, 2, 3) weren't very good for this. To fix this, students in Kaktovik, Alaska, invented these new numerals in 1994. They quickly became popular among the Alaskan Iñupiat and are even being thought about for use in Canada.

The picture next to this text shows the Kaktovik digits from 0 to 19. For bigger numbers, you combine these digits, just like we combine 1 and 0 to make 10. For example, the number twenty is written as a one and a zero (). Forty is a two and a zero (). Four hundred is a one and two zeros (), and so on.

How the Kaktovik System Works

The Iñupiaq language, like other Inuit languages, counts in groups of 20. It also uses smaller groups of 5, 10, and 15 to help. This is similar to how some old European languages counted in "scores" (groups of 20). For example, the number 78 in Iñupiaq is said as three score fifteen-three.

The Kaktovik digits are designed to look like the way Iñupiaq numbers are spoken. For instance, the number seven is called tallimat malġuk in Iñupiaq, which means 'five-two'. The Kaktovik digit for seven looks like a top line (for five) connected to two bottom lines (for two): . This visual connection makes the numbers easier to understand and remember.

Understanding Number Values

The table below shows what each Kaktovik digit means in our regular decimal system. It also shows how their value changes when they are in different places, just like how the '1' in 10 is different from the '1' in 100.

Decimal values of Kaktovik numbers

n	n×203	n×202	n×201	n×200	n×20−1	n×20−2	n×20−3
1	, 8,000	400	20	1	. 0.05	. 0.0025	. 0.000125
2	, 16,000	800	40	2	. 0.1	. 0.005	. 0.00025
3	, 24,000	1,200	60	3	. 0.15	. 0.0075	. 0.000375
4	, 32,000	1,600	80	4	. 0.2	. 0.01	. 0.0005
5	, 40,000	2,000	100	5	. 0.25	. 0.0125	. 0.000625
6	, 48,000	2,400	120	6	. 0.3	. 0.015	. 0.00075
7	, 56,000	2,800	140	7	. 0.35	. 0.0175	. 0.000875
8	, 64,000	3,200	160	8	. 0.4	. 0.02	. 0.001
9	, 72,000	3,600	180	9	. 0.45	. 0.0225	. 0.001125
10	, 80,000	4,000	200	10	. 0.5	. 0.025	. 0.00125
11	, 88,000	4,400	220	11	. 0.55	. 0.0275	. 0.001375
12	, 96,000	4,800	240	12	. 0.6	. 0.03	. 0.0015
13	, 104,000	5,200	260	13	. 0.65	. 0.0325	. 0.001625
14	, 112,000	5,600	280	14	. 0.7	. 0.035	. 0.00175
15	, 120,000	6,000	300	15	. 0.75	. 0.0375	. 0.001875
16	, 128,000	6,400	320	16	. 0.8	. 0.04	. 0.002
17	, 136,000	6,800	340	17	. 0.85	. 0.0425	. 0.002125
18	, 144,000	7,200	360	18	. 0.9	. 0.045	. 0.00225
19	, 152,000	7,600	380	19	. 0.95	. 0.0475	. 0.002375

How the Kaktovik Numerals Were Created

Map of Alaska highlighting North Slope Borough, where the Iñupiat live.

In the early 1990s, something cool happened at Harold Kaveolook school in Kaktovik, Alaska. Students were doing a special math activity. They noticed that their Iñupiaq language used a base-20 counting system. But when they tried to write numbers or do math with the regular Arabic numerals, it was hard because there weren't enough symbols for their numbers.

At first, the students tried making ten extra symbols, but they were too hard to remember. Since there were only nine middle school students in the small town, the whole class could work together. Their teacher, William Bartley, helped them come up with a better idea for a base-20 number system.

The students thought about what a perfect number system should be like. They decided it needed to be:

• Simple to look at: The symbols should be easy to remember.
• Meaningful: The symbols should clearly show what number they mean.
• Quick to write: It should be easy and fast to draw the symbols without lifting your pencil.
• Different: They should look very different from Arabic numerals so there's no mix-up.
• Nice to see: They should look good.

In a base-20 system, the number twenty is written as a '1' followed by a '0'. The Iñupiaq language doesn't have a word for zero. So, the students decided that the Kaktovik digit for zero should look like crossed arms, meaning "nothing is being counted."

When these middle schoolers taught their new numbers to younger students, the younger kids naturally made the numbers fit into a small space. This led to a clever design where the top part of the symbol showed groups of 5, and the bottom part showed the rest. This made doing math much easier to see and understand!

Doing Math with Kaktovik Numerals

An Iñupiaq abacus designed for Kaktovik numerals.

The Kaktovik students found that their new number system made math easier than using Arabic numerals.

Using an Abacus

The students even built special abacuses (counting tools) in their school workshop. These abacuses were made for the base-20 system. They had three beads in the top section for groups of 5 and four beads in the bottom section for the remaining single units. This design helped them convert numbers and do math easily.

Simple Arithmetic

Simple long division using Kaktovik numerals.

Long division with more chunking using Kaktovik numerals.

One cool thing about the Kaktovik system is how simple addition and subtraction look. When you add two digits, their shapes combine to look like the answer!

For example, 2 + 2 = 4 looks like this: + =

Subtraction is even easier. You can just look at a number and visually "remove" the right amount of strokes to get the answer. For example: 4 − 1 = 3 looks like this: − =

Long division also became simpler. The visual design and the groups of five made it almost as easy as short division. Students didn't need to write down many extra steps. They could use different colored pencils to keep track of their work.

Here's a simplified multiplication table for Kaktovik numerals:

×	1	2	3	4		×	1	2	3	4		×	5	10	15
1						5						5
2						10						10
3						15						15
4

To multiply numbers like 6 × 3, you can break down the number 6 into its parts (1 and 5). Then you multiply each part by 3 and add the results: × = ( × ) + ( × ) =

The Impact of Kaktovik Numerals

The Kaktovik numerals have become very popular among the Alaskan Iñupiat. They are now used in language-learning programs. These new numbers have helped bring back the base-20 counting system, which was starting to disappear because of the base-10 system used in English schools.

When the students who created the system moved to high school in Utqiagvik, Alaska (formerly Barrow), they shared their invention. They were allowed to teach it to younger students there. The local Iḷisaġvik College even started offering a course on Inuit mathematics.

In 1996, a group called the Commission on Inuit History Language and Culture officially approved the numerals. Then, in 1998, the Inuit Circumpolar Council in Canada suggested that Kaktovik numerals should be used more in Canada too.

Why These Numerals Are Important

The Kaktovik middle school students showed amazing improvement in their math scores on the California Achievement Test in 1997. Before using the new numerals, their average scores were quite low. After they started using the Kaktovik system, their scores went above the national average! Some people think that being able to work with both base-10 and base-20 systems might help students think about math in more ways, similar to how being bilingual can help you think about the world differently.

Creating their own number system helps Alaskan-native students see that math is a part of their own culture and language. It shows them that math isn't just something from Western culture that you need for college. For students who aren't native, it's a great example of a different way of looking at the world, which is part of studying ethnomathematics (the study of math in different cultures).

Kaktovik Numerals in Computers

The Kaktovik numerals were added to the Unicode Standard in September 2022. This means computers and other devices can now show these numbers correctly. You can find a special computer font for them in the external links section.

Graphical display of Kaktovik Numerals
Official Unicode Consortium code chart: https://www.unicode.org/charts/PDF/U1D2C0.pdf (PDF)

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
U+1D2Cx
U+1D2Dx

See also

• Maya numerals, a base-20 system from another American culture