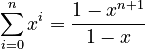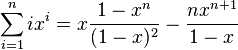List of series facts for kids
A mathematical series is a way of adding up a list of numbers. Sometimes this list is finite, meaning it has a specific end. Other times, the list goes on forever, which we call an infinite series. These series are super useful in many areas of math and science! They help us solve problems and understand patterns.
Contents
Adding Up Powers
Imagine you want to add up all the numbers from 1 to 100. Or maybe you want to add up the squares of those numbers (1² + 2² + 3²...). These are called sums of powers. Mathematicians have found cool formulas to do this quickly!
- Adding up numbers (1, 2, 3...):
If you add up numbers like 1 + 2 + 3 + ... up to a number n, the formula is: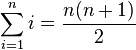 
This is also known as a triangle number because you can arrange dots in a triangle shape with these numbers. For example, 1, 3, 6, 10...
- Adding up squares (1², 2², 3²...):
If you add up the squares of numbers like 1² + 2² + 3² + ... up to n², the formula is: 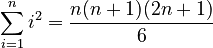Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}\,\!
- Adding up cubes (1³, 2³, 3³...):
If you add up the cubes of numbers like 1³ + 2³ + 3³ + ... up to n³, the formula is: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sum_{i=1}^n i^3 = \left[\frac{n(n+1)}{2}\right]^2\,\! This is interesting because it's just the square of the sum of the numbers themselves!
Power Series: Using x in Sums
Power series are special kinds of sums that include a variable, usually x, raised to different powers (like x⁰, x¹, x², x³...). They are very important for understanding how functions behave.
| Infinite Sum (when x is small) | Finite Sum |
|---|---|
 |
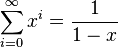This is a Geometric series. It means 1 + x + x² + x³ + ...
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sum_{i=0}^n x^i = \frac{1-x^{n+1}}{1-x}\,\! |
 |
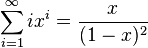This means 1x + 2x² + 3x³ + ...
|
Sums with Factorials
A factorial (written as n!) means multiplying a number by all the whole numbers smaller than it down to 1. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120. Factorials often appear in power series, especially when we are looking at Taylor series which help us approximate functions.
- The number e (Euler's number):
The special number e (about 2.718) can be found using this series: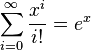 
This means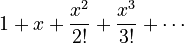 Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots
- Sine and Cosine functions:
The sine and cosine functions, which are used in trigonometry to describe waves and angles, can also be written as infinite series:
-
- Sine (sin x):
-
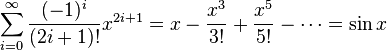
- Cosine (cos x):
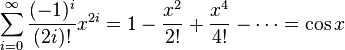
Binomial Series
The Binomial theorem tells us how to expand expressions like (a + x) raised to a power. Binomial series are related to this and are very useful for approximating values.
- Geometric Series (another look):
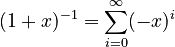Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (1+x)^{-1} = \sum_{i=0}^\infty (-x)^i This is the same as 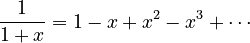Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots when x is small.
- General Binomial Series:
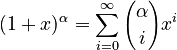Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (1+x)^\alpha = \sum_{i=0}^\infty {\alpha \choose i} x^i This formula works for any number 
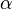(not just whole numbers!) as long as x is between -1 and 1. The 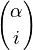Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\alpha \choose i} part is called a binomial coefficient.
Binomial Coefficients: Counting Combinations
Binomial coefficients are numbers that tell you how many ways you can choose a certain number of items from a larger group. They are written as 
and read as "n choose k". They show up in many counting problems and in the binomial theorem.
- Sum of all binomial coefficients:
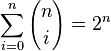If you add up all the ways to choose items from a group of n items (choosing 0, choosing 1, choosing 2, etc.), you get 2 to the power of n. This makes sense because for each item, you either choose it or you don't.
- Binomial Theorem (general form):
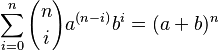This is the famous binomial theorem that helps you expand expressions like (a + b)². For example, (a + b)² = 1a²b⁰ + 2a¹b¹ + 1a⁰b² = a² + 2ab + b². The numbers 1, 2, 1 are the binomial coefficients Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {2 \choose 0} , Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {2 \choose 1} , Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {2 \choose 2} .
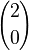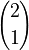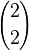Related Topics
